Démontrer que pour tout entiers relatifs a et b on a: si 7 divise a^2 + b^2 alors 7 divise a et 7 divise b
Merci et amusez vous :we:
Arithmétique
10 messages
- Page 1 sur 1
Salut !
Je raisonnerai modulo .
.
Pour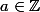 , il n'est pas dur d'établir que
, il n'est pas dur d'établir que  est congru à
est congru à  ou
ou  modulo
modulo  (avec
(avec  si et seulement si
si et seulement si  ).
).
Ainsi, si et seulement si
si et seulement si  et
et  .
.
En effet, pour congrus à
congrus à  ou
ou  modulo
modulo  tels qu'ils ne soient pas tous deux simultanément congrus à
tels qu'ils ne soient pas tous deux simultanément congrus à  modulo
modulo  (i.e. tous deux multiples de 7),
(i.e. tous deux multiples de 7), 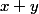 n'est jamais congru à 0 modulo 7 (i.e. n'est jamais un multiple de 7).
n'est jamais congru à 0 modulo 7 (i.e. n'est jamais un multiple de 7).
Après je ne sais pas si tu demandes de l'aide (le "merci") ou si tu proposes ça comme un défi (le "amusez-vous").
:+++:
Je raisonnerai modulo
Pour
Ainsi,
En effet, pour
Après je ne sais pas si tu demandes de l'aide (le "merci") ou si tu proposes ça comme un défi (le "amusez-vous").
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Une autre méthode :
 divise
divise 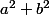 donc on peut trouver
donc on peut trouver  entier relatif tel que
entier relatif tel que 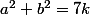 .
.
En cherchant à faire apparaître une identité remarquable, on a^2-2ab=7k) .
.
Ainsi divise
divise 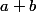 et
et 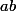 . Or
. Or  est un nombre premier donc par le lemme d'Euclide
est un nombre premier donc par le lemme d'Euclide  divise
divise  ou
ou  divise
divise  .
.
Il suffit alors de distinguer deux cas :
1) Si divise
divise  alors
alors  divise
divise  car on peut écrire
car on peut écrire 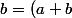-a) ;
;
2) Si divise
divise  alors c'est analogue au cas précédent (
alors c'est analogue au cas précédent ( et
et  jouent des rôles symétriques).
jouent des rôles symétriques).
D'où la conclusion.
:+++:
En cherchant à faire apparaître une identité remarquable, on a
Ainsi
Il suffit alors de distinguer deux cas :
1) Si
2) Si
D'où la conclusion.
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Je raisonnerai modulo.
Pour, il n'est pas dur d'établir que
est congru à
ou
modulo
(avec
si et seulement si
).
Ainsi,si et seulement si
et
.
En effet, pourcongrus à
ou
modulo
tels qu'ils ne soient pas tous deux simultanément congrus à
modulo
(i.e. tous deux multiples de 7),
n'est jamais congru à 0 modulo 7 (i.e. n'est jamais un multiple de 7).
Après je ne sais pas si tu demandes de l'aide (le "merci") ou si tu proposes ça comme un défi (le "amusez-vous").
:+++:
Cette méthode me semble assez claire :lol3:
A la base je demandais de l'aide (d'où le ''merci'') mais pour moi chaque problème de maths est comme un jeu (d'où le ''amusez vous'') :ptdr:
Sur ce, merci :zen:
capitaine nuggets a écrit:Une autre méthode :divise
donc on peut trouver
entier relatif tel que
.
En cherchant à faire apparaître une identité remarquable, on a.
Ainsidivise
et
. Or
est un nombre premier donc par le lemme d'Euclide
divise
ou
divise
.
Il suffit alors de distinguer deux cas :
1) Sidivise
alors
divise
car on peut écrire
;
2) Sidivise
alors c'est analogue au cas précédent (
et
jouent des rôles symétriques).
D'où la conclusion.
:+++:
J'ai suivi ton raisonnement mais j'ai un grand mal à admettre que si (a+b)^2 - 2ab = 7k (k élément de Z) alors 7 divise (a+b) et 7 divise ab :marteau:
Doraki a écrit:si c'était faux tu aurais a et b non multiples de 7 tels que (tout est modulo 7) (b/a)² = -1. Or (b/a)^7 = (b/a) (petit théorème de fermat) donc (b/a étant on nul), 1 = (b/a)^6 = ((b/a)²)^3) = (-1)^3 = -1, contradiction.
Merci pour ta réponse Doraki
Néanmoins, il y a deux trois trucs que je ne comprend pas. Pour moi, si la proposition était fausse, on aurait trois cas à distinguer: ''a et b non multiples de 7'' ou ''a multiple de 7 et b non multiple de 7'' ou ''a non multiple de 7 et b multiple de 7''. Ainsi utiliser la contradiction va impliquer un long raisonnement :marteau:
Maintenant, dans le cas que tu as pris ''a et b non mutilples de 7'', je n'ai pas compris ton raisonnement :mur: :happy2:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
