Un angle aigu+dédicace
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
par yavlory » 17 Fév 2018, 07:04
Bonjour
(je dédicace ce post à Joraan Huu Jordan membre de ce forum depuis peu car c'est lui qui m'a donné l'idée de chercher et trouver le résultat suivant )
Soit
un triangle
posons
,
,
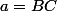
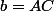
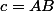
l'angle issu de
du triangle
l'angle issu de
du triangle
l'angle issu de
du triangle
le rayon du cercle circonscrit du triangle
alors en considérant le repère barycentrique
définit selon
)
)
)
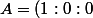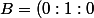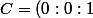et en posant le point
dont les coordonnées barycentriques normalisées par rapport à ce repère barycentrique sont
}{a.b}-\frac {2.R}{a.c} : \frac {1}{c.sin(\alpha)} : 1-\frac {1}{b.tan(\alpha)} \right))
alors on obtient les trois propriétés suivante
CD=1
les droites
)
et
)
sont perpendiculaires
enfin si
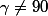
° alors l'angle issu de
du triangle
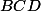
est aigu
sinon
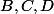
sont alignés
selon
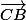
et
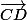
ont même sens (et direction)
-
Magistrat1
- Membre Naturel
- Messages: 27
- Enregistré le: 17 Fév 2018, 10:22
-
par Magistrat1 » 18 Fév 2018, 10:02
Salut, ne le prends pas mal, mais je pense que tu aurais plus de réponse si tu expliquerais mieux je sujet, je veux bien essayer de t'aider, je vais réfléhir, laisse moi un moment, merci d'avance.....
-
Magistrat1
- Membre Naturel
- Messages: 27
- Enregistré le: 17 Fév 2018, 10:22
-
par Magistrat1 » 18 Fév 2018, 10:04
PS : Je pense que tu t'es trompé de lien...
-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
par yavlory » 18 Fév 2018, 13:08
Magistrat1 a écrit:PS : Je pense que tu t'es trompé de lien...
Bonjour
quel lien?
sinon ce sujet ne fait qu'afficher un résultat
il ne pose aucune question
-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
par yavlory » 19 Fév 2018, 07:30
...et si en plus du point
on pose le point
}- \frac {1}{c.tan(\alpha)}: \frac {1}{c.tan(\alpha)}: 1-\frac {1}{b.sin(\alpha)}\right))
alors d'une part on obtient l'équivalence
 \Leftrightarrow \left( C,D,E \mbox { <br /> sont affinement independants} \right))
et d'autre part
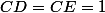
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
