C algébriquement clos

[SimonB]

Autant je suis choqué quand on utilise des trucs d'analyse pour démontrer des trucs algébriques (alors que l'algèbre suffirait)

J'ai récemment vu une preuve purement algébrique du fait que le polynôme caractéristique du produit de deux matrices est égal au polynôme caractéristique du produit dans l'autre sens, uniquement en se plaçant dans le surcorps C[X] (sans utiliser la densité de GL(C)... Je trouve ça franchement magnifique (et diablement incompréhensible) !

[yos]

Et l'anneau des séries formelles A[[X]] est quand même algébrique (même si c'est aussi un complété de A[X] pour la valuation en X), non ?

Je sais pas. Il y a une certaine indépendance entre le procédé de complétion topologique et le procédé de complétion (clôture) algébrique. Il est intéressant de comparer le cas de à celui de R :

Q complétion R cloture algébrique C (et on doit pouvoir permuter les deux opérations).

Q complétion cloture algébrique complétion et ce dernier est algébriquement clos (ouf! On aurait pu continuer longtemps).

Le résultat est "le complété d'un corps valué algébriquement clos de caractéristique 0 est algébriquement clos".
Est-ce que ça s'applique à A[[X]]? Je suis pas bien sûr.

[ffpower]

Alors voici ma demo quasi algebrique:
Soit .On veut montrer que P a un zero.Quitte a remplacer P par ,on peut supposer que les coeff de P sont réels.On fait maintenant une recurrence sur la valuation 2-adique de d=deg(P) (si on écrit ,la valuation 2-adique de d c est a )

Initialisation(a=0):d est donc impair,et un poly reel de degré impair a un zéro réel par le TVI

Supposons avoir prouver que si la valuation 2-adique de d vaut a-1,alors P a des zéros dans C,et supposons maintenant que la valuation 2-adique de d vaut a.Soit les racines de P dans une extension de C.
On veut montrer qu au moins l un des est dans C

Fixons c un réel,et regardons le polynome Q dont les racines sont les .(défini a priori sur une extension de C)
Les coeff de Q sont des poly reels symetriques en donc sont des polys reels en les coeffs de P.(tout poly symetrique est un poly en les fonctions symetriques élémentaires).On en déduit donc que Q est un poly réel,et son degré vaut et est donc de valuation d-adique a-1.On peut donc utiliser la récurrence pour en déduire
qu il existe i,j tel que

Ainsi pour chaque c réel,il existe i,j tel que
Par le principe des tiroirs,on peut trouver c_1 et c_2 pour lesquels correspondent les memes i,j.On a donc


Par manip elementaires,on obtient


et sont donc racines d un poly complexe de degré 2,donc x_i et x_j sont dans C.P a donc un zéro dans C,ce qui acheve la récurrence..

Si des trucs sont pas clairs,n hesitez pas

[ThSQ]

quasi algebrique:..... par le TVI

Mmmm .

[leon1789]

J'ai récemment vu une preuve purement algébrique du fait que le polynôme caractéristique du produit de deux matrices est égal au polynôme caractéristique du produit dans l'autre sens, uniquement en se plaçant dans le surcorps C[X] sans utiliser la densité de GL(C)...

Tu veux dire : dans C[x] ?

Ha oui, c'est exactement le genre de résultat qui, lorsqu'il est accompagné d'une preuve avec un petit argument d'analyse, me fait bondir sur les tables ! Ca y est, je suis énervé............
(je plaisante ThSQ :we: )


Déjà, en admettant ce résultat sur C, on peut démontrer que dans E[x], où E est un anneau commutatif quelconque. C'est donc plus général que cela le laisse entendre dans la formulation (*) !!


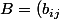Ensuite, comme (**) est un énoncé 100% "polynomial", si on veut s'attaquer à une preuve "directe", i.e. sans passer par le mystificateur corps C, il suffit de le démontrer pour le cas générique de deux matrices A et B sur l'anneau des entiers Z ! Autrement dit, il suffit de montrer l'égalité dans avec et . Il est clair que cela n'a rien à voir avec le corps des nombres complexes C !!!


Bon, pour faire rapide, j'admets l'égalité (valable sur tout anneau commutatif)...
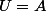
Maintenant, on voit que si A est inversible alors, en posant et , on peut écrire , ce qui donne le résultat .

Or A n'est pas inversible dans , mais l'est dans car son déterminant (le déterminant générique) est non nul, donc inversible.
Donc on établit l'égalité sur le corps .

Cette égalité a lieu évidemment sur , donc dans tout anneau commutatif (par évaluation des matrices génériques). :we:


Certains utiliseront la densité de dans ... Mais ils sont fous ces romains !

Je trouve ça franchement magnifique (et diablement incompréhensible) !

Et maintenant ? :we:

[leon1789]

Alors voici ma demo quasi algebrique (...)

Merci :id:

Mmmm .

Où est le problème ?

Pour démontrer que C est algébriquement clos, il faut bien utiliser qu'il est monté sur R. Donc c'est normal d'utiliser des propriétés valides dans R et C (démontrées bien avant cette démo...), comme
-- >
-- ou bien > (utilisée au début),
-- ou bien > (utilisée au milieu),
-- ou bien > (utilisée à la fin)


Franchement, pour moi, la preuve écrite par ffpower est algébrique. D'ailleurs, on pourrait s'amuser à énoncer

Soit K un corps infini sur lequel tout polynôme de degré impair admet un zéro, et L un surcorps algébrique sur K.
Si tout polynôme de degré deux à coeff dans L admet une racine dans L, alors L est algébriquement clos.

Pour démontrer cela, on relit la démo de ffpower (j'espère ne pas me tromper)... Qui dira que la démo contient un poil d'analyse ?

[SimonB]

Certains utiliseront la densité de dans ... Mais ils sont fous ces romains !

Au niveau prépa en tous cas, c'est pas mal pour se familiariser avec la densité. L'autre preuve est quand même bien plus théorique et un peu "dans la lune" (je ne déteste pas, loin de là !).

Et maintenant ? :we:

... En fait, je connaissais déjà la preuve, c'est l'idée derrière (passer par des polynômes) qui me semble géniale, et en cela "incompréhensible".

[yos]

Moi j'ai pas compris.

il suffit de le démontrer pour le cas générique de deux matrices A et B sur l'anneau des entiers Z ! Autrement dit, il suffit de montrer l'égalité dans l'anneau de polynôme avec et .

Tu veux dire que les matrices A et B sont à coefs dans cet anneau? Mais elle ne sont pas dans cet anneau.

Or A n'est pas inversible dans , mais l'est dans son corps des fractions .
Donc on établit l'égalité sur .

C'est quoi "A inversible dans cet anneau ou corps"?

[ffpower]

Soit K un corps infini sur lequel tout polynôme de degré impair admet un zéro, et L un surcorps algébrique sur K.
Si tout polynôme de degré deux à coeff dans L admet une racine dans L, alors L est algébriquement clos.

Ouais,je pense que ca doit etre vrai.Faut qd meme prouver ceci:
Si L extension algébrique de K et si tout poly de K[x] a un zero dans L,alors L est algébriquement clos.Il doit falloir un peu de Galois pour ca je pense..

ps:on peut réexprimer "tout polynôme de degré deux à coeff dans L admet une racine dans L" plus joliment "L quadratiquement clos"(=tt element de L a une racine carrée dans L")

[ThSQ]

Où est le problème ?

Dire qu'on va faire une démo algébrique et commencer par utiliser le TVI, c'est amusant.
Discussion fort intéressante ...

[leon1789]

Au niveau prépa en tous cas, c'est pas mal pour se familiariser avec la densité.

Certes, c'est vrai.

L'autre preuve est quand même bien plus théorique et un peu "dans la lune" (je ne déteste pas, loin de là !).

Plus théorique ?!?! Là, je ne suis pas d'accord (mais j'ai conscience que les gens en général sont loin de partager mon opinion). Quoi de plus simple qu'une expression polynomiale (, ...) ? ou une fraction rationnelle ? Tout le monde en écrit tout le temps.

... En fait, je connaissais déjà la preuve, c'est l'idée derrière (passer par des polynômes) qui me semble géniale, et en cela "incompréhensible".

Hum, je dirais plutôt :
c'est l'idée derrière (passer par le cas générique) qui me semble naturelle et un coup d'analyse rend la chose "incompréhensible" :we:

[leon1789]

Tu veux dire que les matrices A et B sont à coefs dans cet anneau ? Mais elle ne sont pas dans cet anneau.

oui, elles sont à coefficients dans l'anneau Z[...]

C'est quoi "A inversible dans cet anneau ou corps"?

Arf, je devrais corriger en A inversible dans

[leon1789]

Faut qd meme prouver ceci:
Si L extension algébrique de K et si tout poly de K[x] a un zero dans L,alors L est algébriquement clos.Il doit falloir un peu de Galois pour ca je pense..

Non, seulement de l'algèbre linéaire en dimension finie : soit L/K une extension finie, et . On note l'endomorphisme de multiplication par x. L'application est un morphisme injectif.
Le classique (algèbre linéaire) est traduit en , où (adjoint de x) et (norme de x).

Bref, tout ça pour dire que pour tout , il existe tel que .

Dans notre histoire, on applique ça au polynôme (où L' est le sous-corps de L engendré par les coefficients de P algébriques sur K) : il existe .

ps:on peut réexprimer "tout polynôme de degré deux à coeff dans L admet une racine dans L" plus joliment "L quadratiquement clos"(=tt element de L a une racine carrée dans L")

oups, j'ai utilisé le mot "racine" dans le sens "zéro", pas racine carrée.

[SimonB]

Hum, je dirais plutôt :
c'est l'idée derrière (passer par le cas générique) qui me semble naturelle et un coup d'analyse rend la chose "incompréhensible" :we:

Historiquement, c'est quand même la preuve analytique qui a été la première, me semble-t-il (la preuve algébrique étant due à Chevalley selon mes sources). Est-ce à dire que la compréhension vient après la découverte ?

[leon1789]

Historiquement, c'est quand même la preuve analytique qui a été la première, me semble-t-il (la preuve algébrique étant due à Chevalley selon mes sources). Est-ce à dire que la compréhension vient après la découverte ?

Ben, c'est la preuve que les matheux sont tordus !!! (*)

Cela dit (je relance mon refrain sur les preuves directes), je pense que c'est en reformulant les preuves qu'on comprend mieux parfois...

J'aime bien dire que

le cas générique est un cas particulier qui implique le cas général :marteau:

quand l'énoncé s'y prête bien sûr.

Dire qu'on va faire une démo algébrique et commencer par utiliser le TVI, c'est amusant.
Discussion fort intéressante ...

Dans la phrase >,
il faut considérer > comme un rappel de la preuve de
>.
Pour moi, c'est une autre preuve (d'analyse elle) que celle exposée par ffpower. (*)


______________________
(*)Bon, je m'enfonce... :ptdr:

[yos]

A inversible dans

pourquoi l'est-elle?

[leon1789]

pourquoi l'est-elle?

Son déterminant (le déterminant générique) est non nul.

J'ai corrigé ça aussi :help:

[ffpower]

oups, j'ai utilisé le mot "racine" dans le sens "zéro", pas racine carrée.

J avais bien compris,mais "tout poly de degré 2 est scindé" et "tout elément a une racine carrée",c est equivalant

[leon1789]

J avais bien compris,mais "tout poly de degré 2 est scindé" et "tout elément a une racine carrée",c est equivalant

même quand 2=0 dans le corps de base ?

[yos]

Son déterminant (le déterminant générique) est non nul.

J'ai corrigé ça aussi

Toujours pas...
Si le déterminant de A est non nul, le résultat est évident. Que t'apporte cette restriction du corps de base?