Algèbre : proposition d'exercice.

[Finrod]

Bonjour,

J'y vais aussi d'un exercice en lien avec ce que je fais.

Soit A un anneau intègre. On considère un morphisme

donné par où Q est une série formelle à deux variable sans termes de degrés 0 ou 1.

Montrer que tout morphisme A - linéaire (de module) vérifiant

et

où p est le morphisme A linéaire donné par et

est le morphisme A linéaire donné par



(donc montrer que f)

s'identifie à l'inclusion naturelle de A dans , i.e.

[Finrod]

Mouais, pas très sexy comme exo.

D'ailleurs je ne fais pas le rédiger (c'est pas que mais c'est long)

C'est une récurrence, on note , on vérifie par A-linéarité

On montre a_{0}=1_{A}. Ensuite vérifie une relation de la forme pour tout a, donc comme l'anneau est intègre (sauf si tous les elts de l'anneau sont d'ordre 2...)

Donc là on a utilisé la relation donné ans les hypothèse.

ça donne l'initialisation. On montre ensuite par récurrence que pour tout n, en utilisant la même relation.

Pour info, cela montre que la seule co-action d'un groupe formel A[[t]] sur l'anneau de base A est l'action triviale.

[Doraki]

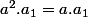
pour tout a,

J'avais l'impression que comme tout était A-linéaire, ça servait à rien de regarder autre chose que m ° f et f[[t]] ° f en 1A (que j'appellerai 1).
Donc ça me surprend de te voir avec un a²

Après simplification, j'ai que si on pose f(1) = 1 + t*P(t),
l'hypothèse dit que (t+u+Q(t,u))*P(t+u+Q(t,u)) = R(t) pour un certain R très moche
Et il faut montrer que P = 0.

Dans le polynôme de gauche, tous les u doivent se simplifier.
Mais comme a gauche on a un polynôme en (t+u+Q), les termes de plus bas degrés sont symétriques en t et u.
Donc il est forcément constant, mais c'est pas possible, sauf si P=0.


En fait,
f[[t]] va de A[[t]] dans A[[t]], et l'image réciproque de A[[t]] par m est A.
Donc si m ° f = f[[t]] ° f, ça fait que f va dans A, et donc f = p ° f = id

[Finrod]

J'avais l'impression que comme tout était A-linéaire, ça servait à rien de regarder autre chose que m ° f et f[[t]] ° f en 1A (que j'appellerai 1).
Donc ça me surprend de te voir avec un a²

Tout a fait.

Je suis allé un peu vite, je vais réparer ça.

Pour le reste, dans la définition de , le est un serie formelle dont l'indéterminé n'est pas à priori t. C'est la même série formelle P mais en la variable u.

Dans tous les cas, l'exo va marcher, il s'agit d'une généralisation d'un truc qui marche bien.

Du coup, faut que je regarde ça !

[Finrod]

Bon alors si on bidouille un peu on va trouver des relations pas trop compliqués entre les coeffs de Q et ceux de P mais ça sert à rien.

J'avais oublié que f vérifie une autre relation, qui dans ce cas, pourtant général, est très simple. C'est juste f(ab)=f(a).f(b).
Donc voilà, c'est à peu prés évident que si f vérifie ça et est A-linéaire, sans utiliser l'autre relation, ça fait 0. L'exo perd son intérêt.
D'où le dans la preuve, c'était un acte manqué.

Les autres truc qu'on peut faire à partir de ça sont trop calculatoires, donc tant pis.

[Doraki]

Donc on doit montrer que si P est dans A[[t]] tel que P(0) = 1 et que P(t+u+Q(t,u)) = P(P(u)*t), alors P = 1 ?

Ben on a toujours qu'on aura forcément un u^n à gauche si P a un terme non constant, et on peut pas en avoir à droite.

[Finrod]

= P(P(u)*t)

En fait c'est juste P(u)P(t)

OK (je viens de comprendre) , désole pour ma dyslexie chronique, mais évidemment, la définition de f[[t]] est hasardeuse. En fait la définition c'est juste f par niveau, donc l'image de P(t) est P(t) P(u). (L'image de t est du coup bien tP(u) mais je ne pensais pas à remplacer t par t P(u) dans le polynôme)

C'est ma faute. Bon après en effet, si ça avait été cette formule, ça aurait annulé les termes en . En particulier le terme devant u, qui vaut 1, donc P aurait été nul.

J'aurais du définir ça comme . Mauvais réflexe. (j'ai voulu faire comme Q qui lui est bien définit comme ça.)