Aide démonstration

[Tanguy]

Bonjour j'aurai besoin d'aide pour résoudre cette démonstration :

module(z^n)=(module(z))n pour tout entier naturel n

arg(zn) = n arg(z) (2pi) pour tout entier naturel n

Démonstration par récurrence sur n entier naturel

Merci pour votre aide

[GaBuZoMeu]

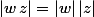
Sais tu que et que ?
Si oui, tu as tout ce qu'il faut pour faire la récurrence. Essaie.

[Tanguy]

Tu pourrai me monter la démonstration complète stp

[GaBuZoMeu]

Je pourrais, mais je ne vais pas le faire : tu n'as jusqu'à présent montré aucun effort de recherche.

Essaie, je t'ai dit. C'est une démonstration par récurrence tout à fait standard (initialisation, hérédité).

[lyceen95]

Connais-tu le principe de la démonstration par récurrence ? En as-tu déjà fait ?
Si tu connais le principe, et si tu connais les 2 propriétés données par GZM, tu as tous les éléments. C'est vraiment l'application très basique du principe de la démonstration par récurrence.