1x2x3x ... = ?

[informaticien]

Bonjour tout le monde
voila, à la base je suis un informaticien, et comme tout informaticien (ou presque) je suis intérssé par les maths. j'ai vu une vidéo qui parle de 1+2+3+ ... = -1/12 de Ramanujan. et une question m'est venue,
si 1+2+3+ ... = -1/12
alors 1x2x3x ... = ?
merci

[aviateur]

Bonjour
1+2+3+ ... = -1/12 de Ramanujan. C'est quoi ce truc?

[informaticien]

Bonjour
1+2+3+ ... = -1/12 de Ramanujan. C'est quoi ce truc?

veuillez voir cette video
https://www.youtube.com/watch?v=jcKRGpMiVTw

[Ben314]

Salut,
C'est la je-sais-pas-combien-ième fois que ça revient sur le tapis cette histoire de 1+2+3+...=-1/12 et je voudrais bien savoir quel est le débile profond qui a mis ça a la mode pour le "grand public" il y a (environ) une dixaine d'année.
Si tu sait pas quoi faire, cherche dans les anales du forum pour retrouver ce qui a été dit sur la question les autres fois que le sujet a été débattus, ou sinon, je te fait la "version courte" :
- Soit tu sait ce qu'est une "fonction holomorphe", un "développement en série entière" ainsi qu'un "prolongement analytique" et on peut effectivement t'expliquer en quel sens la somme 1+2+3+... peut éventuellement être vue comme valant -1/12.
- Soit tu ne sait pas ce que ces termes désignent et là et là, il faut obligatoirement en rester à un niveau "élémentaire" où la vidéo en question, il faut la voir comme ne racontant que des conneries du début à la fin vu que la somme en question il est évident qu'elle tend vers +oo et pas vers autre chose.

P.S. J'ai pas regardé la vidéo vu que, phénomène de mode oblige, ça doit pas être loin d'être le 20em truc que je vois qui parle de la fameuse égalité. Mais si la vidéo parle d'une soit disant "preuve physique" c'est à dire d'un physicien qui aurait utilisé cette fameuse égalité dans un calcul théorique puis vérifié expérimentalement son résultat, ben bien que matheux et pas physicien, je m'était fendu d'aller décortiquer l'article théorique du physicien pour y vérifier que, évidement, il n'utilisait absolument pas cet argument (à savoir 1+2+3+...=-1/12) "brut de décoffrage" pour démontrer son résultat (et heureusement pour lui...)

[capitaine nuggets]

Salut Ben314,

- Soit tu sait ce qu'est une "fonction holomorphe", un "développement en série entière" ainsi qu'un "prolongement analytique" et on peut effectivement t'expliquer en quel sens la somme 1+2+3+... peut éventuellement être vue comme valant -1/12.

Peux-tu m'expliquer ceci stp, je ne connais pas ce point de vue, merci !

[Lostounet]

Salut Ben314,

- Soit tu sait ce qu'est une "fonction holomorphe", un "développement en série entière" ainsi qu'un "prolongement analytique" et on peut effectivement t'expliquer en quel sens la somme 1+2+3+... peut éventuellement être vue comme valant -1/12.

Peux-tu m'expliquer ceci stp, je ne connais pas ce point de vue, merci !

Peut-être regarder du côté du prolongement analytique de Zeta en z=-1

http://www.brouty.fr/Maths/zeta.html

[Ben314]

C'est... tout à fait ça...

Et je ne peut que "plussoyer la conclusion :

Pour en revenir à l'article de départ, il aurait été plus rigoureux de dire que Riemman a trouvé un prolongement analytique à la fonction zeta qui vaut -1/12 pour la valeur -1 de la variable où ce prolongement est défini, mais cela perd de son impact et a l'inconvénient de prendre le lecteur pour un savant, alors les raccourcis qui en mettent plein la vue s'imposent.

Par contre, plus haut, on trouve ça :

Il se trouve que la fonction zéta de Riemann a dans le plan complexe plusieurs prolongements analytiques définis sur le plan auquel on a enlevé le point (1,0). En fait quand on dit plusieurs, c'est dans la formulation car les valeurs pour ces prolongements sont bien évidemment les mêmes;

Et je trouve que le "bien évidement" est franchement de trop vu qu'en général, ben c'est "pas trop" les mêmes.
Le premier exemple de prolongement que l'on voit est en général celui de qui est définie sur le disque de centre 1 et de rayon 1 mais qu'on peut prolonger de façon à définir f(z) pour tout complexe z non nul, sauf que le prolongement n'est pas unique, c'est à dire que la valeur de f(z) va dépendre du trajet qu'on a suivi pour prolonger f de 1 à z...

[capitaine nuggets]

Merci, je ne connaissais pas ce prolongement !

[ffback]

Salut,

Pour répondre á la question initiale, si on veut essayer de donner un sens á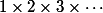 de la même maniére que le tristement classique 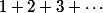, ça m'a l'air faisable:

Soit
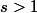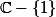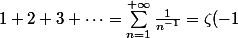La série est apriori definie pour mais en fait converge pour complexe si , ce qui définit une fonction anaytique qui s'étend alors de maniére unique par prolongement analytique sur . On peut alors "considérer que" , et on sait prouver par diverses méthodes analytiques plus ou moins complexes que .

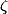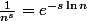Maintenant de la même maniére, si on dérive (en notant que on a, pour :
.
On peut donc considérer que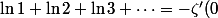 , et on sait prouver que . D'oú , puis en passant á l'exponentielle, .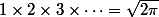

Voilá, donc maintenant qui veut faire des vues peut faire une vidéo expliquant que le produit de tous les entiers vaut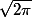 , ça peut faire son petit effet. (par contre ça va plus être difficile á justifier celle lá, même en oubliant toute rigueur...)