Bonjour ! Math QCM

par **rdb** » 07 Sep 2006, 17:57

Bonjour, j'ai quelques problèmes sur ce qcm, si quelqu'un pourrait m'aider ( pas obliger de donner la réponse ^^ ).

a/ Trouvé !!!
b/ R est l'ensemble des solutions de l'inéquation : (-2x+1)(3x+4)<0 (ou egal)
c/ il existe des valuers du réel a telque ax²-V2x+5<0 (V=racinbe carré )
d/ L'équation -x²+mx+1=0 a 2 racines distinctes de signes contraires. => Pas compris ;)
e/ L'équation -x²+mx+1=0 n'admet jamais 2 racines entieres.
Merci de m'aider,
a bientot !

par **fonfon** » 07 Sep 2006, 17:59

Salut,

tableau de signes et discriminant

par **rdb** » 07 Sep 2006, 18:00

Hum... C'est quoi lke discriminant ? :marteau:

par **Oumzil** » 07 Sep 2006, 18:00

t'es en quel niveau ? t'as déjà utilisé les descriminants ?

par **rdb** » 07 Sep 2006, 18:02

Je viens d'entrer en 1ière S :mur:

par **Oumzil** » 07 Sep 2006, 18:04

b/ R est l'ensemble des solutions de l'inéquation : (-2x+1)(3x+4)<0 (ou egal)
à resoudre avec le tableau des signes de -2x+1 et 3x+4

c/ il existe des valuers du réel a telque ax²-V2x+5<0 (V=racinbe carré )
factorisation et tableau des signes

le reste factorise le trinome et prouves que les racines sont des quotient irreductibles

par **rdb** » 07 Sep 2006, 18:06

Je sait qu'il faut factoriser, mais je me trompe toujours dans mes calculs....

par **fonfon** » 07 Sep 2006, 18:08

Re,

une equation du second degré est de la forme ax²+bxc=0 (a#0, x inconnue).
Les eventuelles solutions de l'equation sont aussi appelées les racines ou zéros du polynôme.
on pose: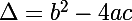

(appelé discriminant du polynôme)

SI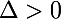

l'equation a 2 solutions distinctes:

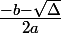ou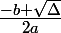

Si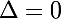

l'equation a une solution double :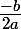

Si

l'equation n'a pas de solutions réelles, mais admet 2 solutions complexes

par **Oumzil** » 07 Sep 2006, 18:08

c/ il existe des valuers du réel a telque ax²-V2x+5<0 (V=racinbe carré )
dis moi c'est racine de 2 fois x ou racine de deux x

par **Oumzil** » 07 Sep 2006, 18:09

fonfon lé en 1 ère jcrois pas qu'il connait les nombres complexes bon moi aussi je les connais pas encore

par **rdb** » 07 Sep 2006, 18:11

Désolé Ouzmil, c'est racine2 X x
Fonfon, je peux donc utiliser le discriminant pour c/, d/, et e/ ?

par **fonfon** » 07 Sep 2006, 18:24

Fonfon, je peux donc utiliser le discriminant pour c/, d/, et e/ ?

je sais pas si tu ne le connais pas encore, sinon il faut en effet que tu factorise, tu connais peut-être la forme canonique

par **rdb** » 07 Sep 2006, 18:24

Encore besoin d'aide, comment utilisre le discriminant ?

par **rdb** » 07 Sep 2006, 18:25

Forme canonique c'est (a+b)²+c ?

par **Clembou** » 07 Sep 2006, 18:32

rdb a écrit:Bonjour, j'ai quelques problèmes sur ce qcm, si quelqu'un pourrait m'aider ( pas obliger de donner la réponse ^^ ).

a/ Trouvé !!!
b/ R est l'ensemble des solutions de l'inéquation : (-2x+1)(3x+4) Pas compris
e/ L'équation -x²+mx+1=0 n'admet jamais 2 racines entieres.
Merci de m'aider,
a bientot !

Alala ! On se perd dans ces termes : discriminants, forme canonique (et bientôt dérivée)....

Il est clair qu'il faut utiliser la méthode des discriminants pour le c - d et e. Quoique le c peut se résoudre assez facilement.

c)

Impossible car

par **fonfon** » 07 Sep 2006, 18:40

Re,

la forme canonique d'un trinôme de la forme ax²+bx+c (a,b,c réels, a#0) est:

par **rdb** » 07 Sep 2006, 19:30

Merci beaucoup, je verrai ca demain car je suis saturé en math la ^^.
En fait, sinon ce qui me gène le plus c'est les deux inconnus.

par **Oumzil** » 07 Sep 2006, 20:15

[quote="Clembou"]Alala ! On se perd dans ces termes : discriminants, forme canonique (et bientôt dérivée)....

Il est clair qu'il faut utiliser la méthode des discriminants pour le c - d et e. Quoique le c peut se résoudre assez facilement.

c) [tex]\exist a \in \mathbb{R} | ax^2-\sqrt{2}x+5 0
alors ax²+\sqrt{2}x + 5 a deux racines dans IR
soit x_1 et x_2 ces deux racines tel que x_1 < x_2
on a pour tout x de l'intervalle [x_1 ; x_2] ax²+ (racine de 2)* x + 5 < 0

par **Oumzil** » 07 Sep 2006, 23:26

je suis pas trop sur de ce que tu as dis clembo

par **Oumzil** » 08 Sep 2006, 14:59

:marteau: :dodo: :doh:

Bonjour ! Math QCM

Bonjour ! Math QCM

Qui est en ligne