Démontrer que Béta est injective et surjective
33 messages
- Page 1 sur 2 - 1, 2
Démontrer que Béta est injective et surjective
jour,
Voici l'énoncé:
Soient A et B deux parties d'un ensemble E, on définit l'application Béta de P(E) dans le produit cartésien P(A)xP(B) par:
Pour tout x P(E), Béta = (XnA, XnB) [n pour inter]
==> déterminer les couples images de Béta de E, de "ensemble vide", de Abarre et de AUB
==> j'ai montré que selon les résultats que l'on obtenait, Béta n'est pas injective.
Mais ils me demandent de donner une condition nécessaire pour que Béta soit injective.
J'ai pensé à ça:
il faut que X A et que X B ==> Est-ce correcte? existe-t-il une autre condition?
Vous en remerciant par avance pour tout conseil apporté
Voici l'énoncé:
Soient A et B deux parties d'un ensemble E, on définit l'application Béta de P(E) dans le produit cartésien P(A)xP(B) par:
Pour tout x P(E), Béta = (XnA, XnB) [n pour inter]
==> déterminer les couples images de Béta de E, de "ensemble vide", de Abarre et de AUB
==> j'ai montré que selon les résultats que l'on obtenait, Béta n'est pas injective.
Mais ils me demandent de donner une condition nécessaire pour que Béta soit injective.
J'ai pensé à ça:
il faut que X A et que X B ==> Est-ce correcte? existe-t-il une autre condition?
Vous en remerciant par avance pour tout conseil apporté
A mon avis ta solution est suffisante, mais pas nécessaire. Je n'y ai réfléchis qu'un tout petit coup, donc excuse-moi si je fais une erreur, mais je te propose de raisonner de la façon suivante:
Tu divise les éléments de X en quatre catégorie: 1) les éléments qui sont ni dans A ni dans B, 2) les éléments qui ne sont que dans A, 3) les éléments qui ne sont que dans B et 4) les éléments qui sont dans A et B. Ca donne:
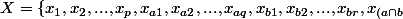1}, x_{(a\cap b)2},..., x_{(a\cap b)s}\}) , si tu comprends la logique.
, si tu comprends la logique.
Ainsi tu as:=(\{x_{a1}, x_{a2}, ..., x_{aq}, x_{(a\cap b)1}, x_{(a\cap b)2},..., x_{(a\cap b)s}\},\{ x_{b1}, x_{b2},..., x_{br}, x_{(a\cap b)1}, x_{(a\cap b)2},..., x_{(a\cap b)s}\}))
Qu'est-ce qu'il se passe quand tu ajoutes ou supprimes un des éléments de la forme ? Et un de la forme
? Et un de la forme  ? Et un de la forme...
? Et un de la forme...
Tu divise les éléments de X en quatre catégorie: 1) les éléments qui sont ni dans A ni dans B, 2) les éléments qui ne sont que dans A, 3) les éléments qui ne sont que dans B et 4) les éléments qui sont dans A et B. Ca donne:
Ainsi tu as:
Qu'est-ce qu'il se passe quand tu ajoutes ou supprimes un des éléments de la forme
WhiteShadow a écrit:A mon avis ta solution est suffisante, mais pas nécessaire. Je n'y ai réfléchis qu'un tout petit coup, donc excuse-moi si je fais une erreur, mais je te propose de raisonner de la façon suivante:
Tu divise les éléments de X en quatre catégorie: 1) les éléments qui sont ni dans A ni dans B, 2) les éléments qui ne sont que dans A, 3) les éléments qui ne sont que dans B et 4) les éléments qui sont dans A et B. Ca donne:, si tu comprends la logique.
Ainsi tu as:={x_{a1}, x_{a2}, ..., x_{aq}, x_{(a\cap b)1}, x_{(a\cap b)2},..., x_{(a\cap b)s}, x_{b1}, x_{b2},..., x_{br}, x_{(a\cap b)1}, x_{(a\cap b)2},..., x_{(a\cap b)s}})
Maintenant, si tu enlèves ou rajoute des éléments de la formedans X (on appelle le nouvel ensemble X1), tu as bêta(X)=bêta(X1). Donc bêta n'est pas injective.
Par contre, dès que tu modifies un seul élément de A ou B, ton bêta(X) change. Donc à mon avis ta solution nécessaire est de restreindre X à
si beta est inj tu as beta(C)=vide=beta de vide donc C=vide
il n'y a donc pas d'elements dasn ta categorie 1
reciproquement beta(X)=beta(Y) =>
or C=vide ssi E=AUB donc tuas bien pour tout X,Y beta(X)=beta(Y) => X=Y
cpS a écrit:OK. Mais si j'avais fait comme proposition:
X et A ET X et B ne soient pas disjoints?
Non, là par contre tu fais faux.
Si tu prends X1 et X2, qui ne sont ni disjoints avec A, ni disjoints avec B. Tu rajoutes comme hypothèse que
Tu as alors: X1
Donc bêta n'est pas injective.
WhiteShadow a écrit:Non, là par contre tu fais faux.
Si tu prends X1 et X2, qui ne sont ni disjoints avec A, ni disjoints avec B. Tu rajoutes comme hypothèse queet
. Par contre, on pose qu'ils ont des éléments qui ne sont ni dans A ni dans B différents, autrement dit X1 n'est pas égal à X2.
Tu as alors: X1X2. Mais
=beta(X2))
Donc bêta n'est pas injective.
si E=AUB, il n'y a pas d'elements qui ne soient ni dans A ni dans B
WhiteShadow a écrit:Non, là par contre tu fais faux.
Si tu prends X1 et X2, qui ne sont ni disjoints avec A, ni disjoints avec B. Tu rajoutes comme hypothèse queet
. Par contre, on pose qu'ils ont des éléments qui ne sont ni dans A ni dans B différents, autrement dit X1 n'est pas égal à X2.
Tu as alors: X1X2. Mais
=beta(X2))
Donc bêta n'est pas injective.
Donc quelle condition dois-je donc poser pour que Béta soit injective? Je ne vois pas.
WhiteShadow a écrit:Exact! Et là tu as ta réponse. En tout cas à mon avis... :ptdr:
Donc pour l'injection,
la condition est : E=AUB
Mais pour la surjection,
On me demande d'étudier l'existence d'un antécédent par Béta du couple('ensemble vide', B)
ensuite, je dois déterminer la condition nécessaire pour que Béta soit surjective, et démontrer que cette condition est suffisante.
Est-ce que si je mets que la condition est: E=A=B c'est correct? :doh:
33 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
