Exercice

[maths0]

Dis moi ce que tu ne comprends pas, si je peux t'aider à progresser ce sera avec plaisir ? J'attends

Ce que tu ne comprends pas c'est qu'il n'arrive pas à assimiler ce qu'est une relation de proportionnalité alors arrête de te faire plaisir avec des racines déjà que cette relation il ne l'assimile pas ....
Tu mets des k des k', qu'est ce que cela signifie pour lui ? Rien tu le perds !
Mais ce n'est pas grave la pédagogie cela s'apprend, tu peux garder l'espoir.

[triumph59]

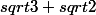
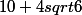
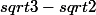
Le tableau est proportionnel si tu passes de à en multipliant par k et si tu passes de à 2 en multipliant par la même valeur k

Tu calcules k pour le 1er cas
k=
k=
k=
k=
k=
k=
k=
k=

[lemosellan57800]

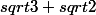
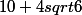
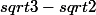
Le tableau est proportionnel si tu passes de à en multipliant par k et si tu passes de à 2 en multipliant par la même valeur k

Tu calcules k pour le 1er cas
k=
k=
k=
k=
k=
k=
k=
k=

Je marque que sa??

[triumph59]

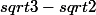
Tu calcules k' de la même façon entre et 2

k'=
k'=

en utilisant la même identité remarquable que tout à l'heure =1

k'=

k=k' et donc le tableau est proportionnel

[maths0]

En répétant pour pouvoir suivre les étapes :

[CENTER] [/CENTER]

Car :
[CENTER][/CENTER]

J'aime bien, tu progresses vite :lol3:
C'est parfait.

[lemosellan57800]

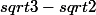
Tu calcules k' de la même façon entre et 2

k'=
k'=

en utilisant la même identité remarquable que tout à l'heure =1

k'=

k=k' et donc le tableau est proportionnel

Merci beaucoup a tous les deux

[triumph59]

Ce que tu ne comprends pas c'est qu'il n'arrive pas à assimiler ce qu'est une relation de proportionnalité alors arrête de te faire plaisir avec des racines déjà que cette relation il ne l'assimile pas ....
Tu mets des k des k', qu'est ce que cela signifie pour lui ? Rien tu le perds !
Mais ce n'est pas grave la pédagogie cela s'apprend, tu peux garder l'espoir.

Tu crois qu'à jouer avec des approximations tu y gagnes quelque chose ?

[maths0]

Tu crois qu'à jouer avec des approximations tu y gagnes quelque chose ?

La compréhension et c'est ce qu'il y a de plus chère au monde :zen:.
Il ne connait pas ses règles de distribution et de simplification..... à bon entendeur.

[triumph59]

Dans ce cas tu vas lui démontrer que Pi=22/7 car en arrondissant Pi à 3.14 et 22/7 à 3.14 j'ai le même résultat

Il faut être sérieux parfois ne penses-tu pas ?

[maths0]

Dans ce cas tu vas lui démontrer que Pi=22/7 car en arrondissant Pi à 3.14 et 22/7 à 3.14 j'ai le même résultat

Il faut être sérieux parfois ne penses-tu pas ?

Tu n'as rien compris et tu ne peux pas comprendre, tu peux rester dans ta caverne (Platon).

[maths0]

Dans ce cas tu vas lui démontrer que Pi=22/7 car en arrondissant Pi à 3.14 et 22/7 à 3.14 j'ai le même résultat

Il faut être sérieux parfois ne penses-tu pas ?

Tu es en train d'insulter ceux qui ont inventé le symbole environ égal !