Système d'équation du premier degré à 2 variables.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 15 Fév 2013, 14:45
par Maxelanus » 15 Fév 2013, 14:45
Bonjour, est-ce qu'il y a une méthode simple à savoir pour bien réaliser des système d'équation du premier degré à 2 variables ?
Par exemple j'ai ici ;
'' Le tiers d'un nombre plus le quart d'un autre totalisent 28. Le neuvième de leur somme est égal à 11. ''
Donc, x/3 + y/4 = 28 ?
Est-ce qu'il y a une méthode pour faire ça ? Un produit croisé ou je ne sais pas.
Merci à vous.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 14:54
par ampholyte » 15 Fév 2013, 14:54
Bonjour,
Tu dois utiliser les deux hypothèses donc tu obtiens un système de 2 équations à 2 variables que tu as déjà dû apprendre à résoudre !
x/3 + y/4 = 28
(x + y)/9 = 11
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 15 Fév 2013, 14:55
par Maxelanus » 15 Fév 2013, 14:55
Dans un problème du genre, doit-il toujours avoir 2 équations ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 14:58
par ampholyte » 15 Fév 2013, 14:58
Oui, car tu ne peux pas résoudre une équation à 2 inconnues.
Il faut au moins n équations pour résoudre un système à n inconnues.
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 15 Fév 2013, 14:59
par Maxelanus » 15 Fév 2013, 14:59
D'accord.
Le (x + y)/9 = 11.
Lui me mélange un peu, est-ce que ça donne quelque chose du genre ?
x/9 + y/9 = 11 ?
Je ne connais pas la valeur de ni x ni y, c'est ce qui me bloque un peu.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 15:05
par ampholyte » 15 Fév 2013, 15:05
Il faut que tu utilises la méthode par substitution
Tu as le système suivant :
/9 = 11<br />\end{array}<br />\right)
Substitution

Donc
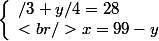
On remplace x dans la première expression
/3 + y/4 = 28 \\<br />x = 99 - y<br />\end{array}<br />\right)
Tu peux donc déterminer y, puis x
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 15 Fév 2013, 15:18
par Maxelanus » 15 Fév 2013, 15:18
Comment as-tu déterminé que x+y = 99 ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 15:24
par ampholyte » 15 Fév 2013, 15:24
(x + y)/9 = 11
x + y = 11*9 = 99
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 15 Fév 2013, 15:27
par Maxelanus » 15 Fév 2013, 15:27
Ah oui, je comprend.
(x + y)/9 = 11
x/9 + y/9 = 11 *9
(x + y) = 99.
Donc nous avons multiplié par 9 pour annuler les fractions. Exact ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 15:53
par ampholyte » 15 Fév 2013, 15:53
C'est exacte.
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 17 Fév 2013, 17:00
par Maxelanus » 17 Fév 2013, 17:00
Besoin de clarification ici assez rapidement merci.
J'ai atteint ce résultat ->
x/3 + y/4 = 28
(x + y)/9 = 11 ----> x + y = 11*9 = 99
x/3 + y/4 = 28
x = 99 - y
( (99 - y)/3 + y/4 = 28 ) * 3
( 297 - 3y + 3y/4 = 84 ) *4
1188 - 12y + 12y = 336.
Ensuite, comment puis-je isoler y ?
-12y + 12y = 336 - 1188
y = -852 ?
Le chiffre semble un peu elevé non ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 17 Fév 2013, 20:40
par ampholyte » 17 Fév 2013, 20:40
Tu as une erreur ici :
( (99 - y)/3 + y/4 = 28 ) * 3
( 297 - 3y + 3y/4 = 84 ) *4
( (99 - y)/3 + y/4 = 28 ) * 3
( 99 - y + 3y/4 = 84 ) *4
396 -4y + 3y = 336
y = 396 - 336 = 60
On remplace ensuite dans
x = 99 - y
x = 99 - 60 = 39
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 17 Fév 2013, 21:12
par Maxelanus » 17 Fév 2013, 21:12
Pourquoi est-ce que ( (99 - y)/3 + y/4 = 28 ) * 3 ne te donne pas 297 ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 17 Fév 2013, 21:48
par Lostounet » 17 Fév 2013, 21:48
ampholyte a écrit:Oui, car tu ne peux pas résoudre une équation à 2 inconnues.
Il faut au moins n équations pour résoudre un système à n inconnues.
Hihi, pas toujours ! (Merci olympus):
^2 + (y +1)^2 = 0)
a des solutions bien déterminées x = 2 et y = -1 !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 18 Fév 2013, 09:11
par ampholyte » 18 Fév 2013, 09:11
Ba n'oublie pas que si tu multiplies par 3, tu auras 99/3 * 3 = 99
-
Maxelanus
- Membre Naturel
- Messages: 38
- Enregistré le: 16 Jan 2013, 18:21
-
 par Maxelanus » 18 Fév 2013, 16:03
par Maxelanus » 18 Fév 2013, 16:03
Ah mais oui... Tu as raison.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
