Exo proba
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wemi
- Membre Naturel
- Messages: 49
- Enregistré le: 11 Juin 2005, 13:16
-
 par Wemi » 11 Aoû 2006, 18:38
par Wemi » 11 Aoû 2006, 18:38
je bloque sur une question de cette exo:
Une voiture participe à une course automobile qui se déroule sur un circuit fermé en un nombre fini de tours(au moins 2). Pour N>=1, on note

la variable aléatoire égale à 1 si la voiture arrive en tête au nième touret à 0 sinon. On pose
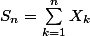
et on suppose de plus que
=p)
(p]0,1[) et
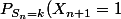=\frac{k+1}{n+1})
J'ai montré que
=\frac{1}{n+1}+\frac{E(S_n)}{n+1})
J'ai dû déterminé la loi de

J'obtiens
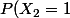=\frac{p+1}{2})
et pour
=\frac{1-p}{2})
Après on me demande de montrer que tous les
)
suivent la même loi.
Je bloque, j'ai pensé à une récurence mais j'en suis toujours au même point.
Pouvez-vous m'aider svp?
merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Aoû 2006, 18:57
par tize » 11 Aoû 2006, 18:57
Il y a pas mal de chose qui ne sont pa très claires pour moi dans ton énoncé :
que signifie :
et aussi :
-
Wemi
- Membre Naturel
- Messages: 49
- Enregistré le: 11 Juin 2005, 13:16
-
 par Wemi » 11 Aoû 2006, 19:01
par Wemi » 11 Aoû 2006, 19:01
tize a écrit:Il y a pas mal de chose qui ne sont pa très claires pour moi dans ton énoncé :
que signifie :
et aussi :
pour la première, cela signifie la proba que X_(n+1)=1 sachant Sn=k
et pour la deuxième, c'est un oubli, j'ai édité
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Aoû 2006, 19:49
par tize » 11 Aoû 2006, 19:49
Avec une recurrence ça marche bien :
Si
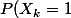=\frac{p+1}{2})
pour
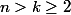
alors
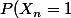=\frac{1}{n+1}+\frac{E(S_n)}{n+1}=\frac{1}{n+1}+\frac{\sum_{k=1}^{n}E(X_k)}{n+1}=\frac{1}{n+1}+\frac{p+(n-1)\frac{p+1}{2}}{n+1})

est l'esperance de

et les
)
autre variables ont la même esperance (par récurrence)
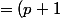/2)
-
Wemi
- Membre Naturel
- Messages: 49
- Enregistré le: 11 Juin 2005, 13:16
-
 par Wemi » 11 Aoû 2006, 19:52
par Wemi » 11 Aoû 2006, 19:52
tize a écrit:Avec une recurrence ça marche bien :
je vois pas trop, les Sn me gênent
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Aoû 2006, 19:56
par tize » 11 Aoû 2006, 19:56
j'ai modifier mon dernier post !
Il ne faut pas oublier que l'esperance est lineaire.
Il ne reste plus qu'à simplifier...
-
Wemi
- Membre Naturel
- Messages: 49
- Enregistré le: 11 Juin 2005, 13:16
-
 par Wemi » 12 Aoû 2006, 09:21
par Wemi » 12 Aoû 2006, 09:21
:++: merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
