Céviennes isotomiques

[Zweig]

Salut,

On appelle cévienne d'un triangle ABC toute droite D contenant un sommet de ce triangle et sécante avec le côté opposé. Le point où D coupe le côté opposé est dit pied de la cévienne D.
Deux céviennes D et D' issues d'un même sommet sont dites isotomiques lorsques leurs pieds sont symétriques par rapport au milieu du côté opposé.

Montrer que les céviennes isotomiques de trois céviennes concourantes ou parallèles sont elles-mêmes trois céviennes concourantes ou parallèles.

http://www.noelshack.com/2012-27-1341581561-ceviennes_isotomiques.png

[chan79]

Salut,

On appelle cévienne d'un triangle ABC toute droite D contenant un sommet de ce triangle et sécante avec le côté opposé. Le point où D coupe le côté opposé est dit pied de la cévienne D.
Deux céviennes D et D' issues d'un même sommet sont dites isotomiques lorsques leurs pieds sont symétriques par rapport au milieu du côté opposé.

Montrer que les céviennes isotomiques de trois céviennes concourantes ou parallèles sont elles-mêmes trois céviennes concourantes ou parallèles.

http://www.noelshack.com/2012-27-1341581561-ceviennes_isotomiques.png

pour les concourantes, on y arrive avec le théorème de Ceva

[Zweig]

Pour les parallèles aussi ... J'attendais néanmoins une autre solution (c'est un peu trop expéditif avec le théorème de Céva :lol3:)

[chan79]

Pour les parallèles aussi ... J'attendais néanmoins une autre solution (c'est un peu trop expéditif avec le théorème de Céva :lol3:)

On peut le faire par l'analytique en plaçant un repère mais c'est vraiment rébarbatif ...
Au fait, les céviennes isotomiques de trois céviennes parallèles peuvent-elles être parallèles ou sont-elles toujours concourantes ?

[utwa]

Bonjour,

On part d'un "vrai" triangle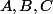 ayant trois sommets non alignés et à distance finie. On ajoute un quatrième point que l'on définit par ses coordonnées barycentriques. Cela donne :

[CENTER][/CENTER]

Lorsque , cela veut tout bonnement dire que est le barycentre des points 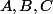pour les masses 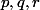. Sinon, il s'agit du point à l'infini dans la direction du vecteur (direction qui est indépendante du choix d'une origine ).

La -cevienne du point est, par définition, la droite 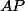. Les coefficients de son équation se calculent à vue. On peut aussi les obtenir en posant

[CENTER][/CENTER]

Les coordonnées du point . se calculent à vue. On peut aussi les obtenir en posant

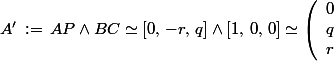[CENTER][/CENTER]

On définit de meme . Puis on prend les symétriques de ces points par rapport au milieu du côté adéquat. Pour 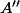, cela revient à permuter les pondérations des points 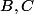. Cela donne

[CENTER][/CENTER]

On voit donc que les points sont les céviens du point . Ce point que l'on note aussi est appelé conjugué isotomique du point .

La conjugaison isotomique, c'est à dire est une transformation involutive ... à condition de ne pas regarder ce qui se passe lorsque l'un des points est sur l'un des côtés du triangle.

Cordialement.