Trigonométrie !!

[RedRose]

Salut les Amiis !
J'ai vraiment besoin de votre aide pour démontrer un truc qui parait peut être simple mais que j'arrive pas à prouver :

Démontrer que -;)2 Merci

[gdlrdc]

Connais-tu la formule de trigo:
cos(a-b)=cosacosb+sinasinb ?
Tu pourrais t'en servir avec a=x et b=pi/4

[RedRose]

Connais-tu la formule de trigo:
cos(a-b)=cosacosb+sinasinb ?
Tu pourrais t'en servir avec a=x et b=pi/4

Heu .. Non, Je pense que j'utiliserai sin²x + cos²x =1 et l'indentité remarquable ( sinx + cosx)²

[manoa]

Heu .. Non, Je pense que j'utiliserai sin²x + cos²x =1 et l'indentité remarquable ( sinx + cosx)²

en effet ..

ton inigalité est équivalante à |sinx+cox|< utilise l'identité, développe, et utilise cette propriété que tu dois connaitre : |sinx|<=1 et |cosx|<=1 pour tous x de R

[gdlrdc]

Oui ça marche aussi avec cos^2+sin^2 =1:
mais attention l'inégalité que tu as écrite n'est pas stricte.

sinon tu avais :
cos(x-pi/4)=cosxcospi/4+sinxsinpi/4 et comme cospi/4=sinpi/4=1/;)2
cela donne: cosx+sinx=;)2 cos(x-pi/4)
et tu conclus car cos appartient à [-1,1].

[RedRose]

Oui ça marche aussi avec cos^2+sin^2 =1:
mais attention l'inégalité que tu as écrite n'est pas stricte.

sinon tu avais :
cos(x-pi/4)=cosxcospi/4+sinxsinpi/4 et comme cospi/4=sinpi/4=1/;)2
cela donne: cosx+sinx=;)2 cos(x-pi/4)
et tu conclus car cos appartient à [-1,1].

Meme resultat ! Racine 2 . Cos(x-pi/4) est compris entre racine 2 et moins racine 2 !
Alors C'est la meme chose pour cos x + sin x
Non ?

[chan79]

Meme resultat ! Racine 2 . Cos(x-pi/4) est compris entre racine 2 et moins racine 2 !
Alors C'est la meme chose pour cos x + sin x
Non ?

On peut étudier les variations de f(x)=sin(x)+cos(x)

[globule rouge]

Meme resultat ! Racine 2 . Cos(x-pi/4) est compris entre racine 2 et moins racine 2 !
Alors C'est la meme chose pour cos x + sin x
Non ?

Nan, justement, ce qu'on essaie de te dire c'est que donc …
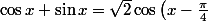Comme , nous avons l'encadrement !
Je ne fais que répéter mot pour mot que ce qui a été dit ^^

Julie

[Elerinna]

On peut étudier les variations de f(x)=sin(x)+cos(x)

L'étude des variations de la fonction sur est une manière analytique rapide ainsi que la méthode géométrique