[L1] Polynômes et nombres de Bernoulli.

[ev85]

Alors, je me lance... du moins, j'essaie...

D'après Taylor :



Et :
Avec p=n-k, on a :
Avec p=k, on a :



D'où :

OK !

Maintenant, il s'agit de trouver ton égalité.

e.v.

[Deluxor]

OK !

Maintenant, il s'agit de trouver ton égalité.

e.v.

Oui...

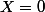
Peux-tu m'expliquer pourquoi on se place en , alors que le résultat attendu est : ?

[ev85]

Oui...

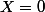
Peux-tu m'expliquer pourquoi on se place en , alors que le résultat attendu est : ?

Ecris les formules de Taylor de ces deux polynômes, tu poseras les questions métaphysiques après !

e.v.

[Deluxor]

, d'où :


Donc :

[ev85]

, d'où :


Donc :

C'est un peu succinct comme formule de Taylor. Du coup , ça ne donne qu'un résultat très partiel. Allez, un petit effort et donne moi les vraies formules de Taylor.

[Deluxor]

Je suis désolé, je ne vois pas...
La formule de Taylor que j'avais dans mon cours était celle que j'ai utilisé auparavant.
Un coup de pouce? ^^

[Deluxor]

J'ai finalement réussi cette question (et le reste, jusqu'à la question 7b).

Quelqu'un peut-il m'aider pour la question 7b?

[ev85]

Je suis désolé, je ne vois pas...
La formule de Taylor que j'avais dans mon cours était celle que j'ai utilisé auparavant.
Un coup de pouce? ^^

Nan ! Je t'ai demandé d'écrire les formules de Taylor pour chacun des polynômes et n. et tu ne l'as pas fait.

[Deluxor]

ev85, j'ai finalement fait comme ça :

[ev85]

ev85, j'ai finalement fait comme ça :

OK, tu as le droit de poser tes questions métaphysiques !

[Deluxor]

OK, tu as le droit de poser tes questions métaphysiques !

Lol, du coup, par cette méthode, je n'en ai pas... ^^

Pour la 7a), j'ai fait une intégration par parties, et ça a bien marché.
Pour la b), je suppose qu'il faut utiliser la question a), mais je ne vois pas ce qu'il faut faire. Récurrence sur k?

[ev85]

Lol, du coup, par cette méthode, je n'en ai pas... ^^

Pour la 7a), j'ai fait une intégration par parties, et ça a bien marché.
Pour la b), je suppose qu'il faut utiliser la question a), mais je ne vois pas ce qu'il faut faire. Récurrence sur k?

ça sent la récurrence sur k et l'IPP.

[Deluxor]

Je voyais bien ça comme ça aussi...
J'initialise donc à k=1, puis je suppose l'égalité vraie pour k compris entre 1 et p?

[ev85]

Je voyais bien ça comme ça aussi...
J'initialise donc à k=1, puis je suppose l'égalité vraie pour k compris entre 1 et p?

ça devient une récurrence sur p !

Pourquoi pas k=0 ?

[Deluxor]

Comme la question nous dit pour tout entier k de l'intervalle [1;p], je pensais qu'il fallait initialiser à k=1?

Et en initialisant à k=0, on a du ...

[ev85]

Comme la question nous dit pour tout entier k de l'intervalle [1;p], je pensais qu'il fallait initialiser à k=1?

Et en initialisant à k=0, on a du ...

Ah, au temps pour moi. Donc récurrence et deux IPP.

[Deluxor]

J'ai initialisé.

L'égalité me fait tellement peur que je ne sais par où la prendre...
De l'hypothèse de récurrence? Du résultat au rang k+1?
Sur quoi faire l'IPP?

[ev85]

J'ai initialisé.

L'égalité me fait tellement peur que je ne sais par où la prendre...
De l'hypothèse de récurrence? Du résultat au rang k+1?
Sur quoi faire l'IPP?

Bonjour Deluxor.

Si tu as peur des calculs, les maths c'est pas une bonne idée.
D'autant plus que là ce n'est pas bien terrible.

Tu vas commencer par refaire soigneusement la démonstration de la formule de Taylor avec reste intégral. C'est la même chose. La seule différence c'est un choix différent des primitives.
Ensuite tu vas faire tes IPP. Le choix de la fonction à dériver est évident et celui de la fonction à primitiver est guidé par les premières questions.

Un peu de courage que diantre ! Je ne vais pas faire les calculs à ta place.