Oral type X-ENS

par **abel** » 06 Juin 2006, 17:07

Bonjour à tous.
Voilà je sèche sur une planche de X-ENS depuis 2-3h et j'aimerais bien que quelqu'un m'aide à demarrer. Sachant que je sais que cet exo présente des aspcts un peu trop limite du programme mais il est quand meme abordable parait-il.Voilà l'énoncé :

symétriques avec

(erreur corrigée)

Montrer que :

Etudier le cas d'égalité.

Moi j'ai bien sûr exploité la diagonalisabilité de A mais je ne vois pas comment exploiter celle de B en meme tps. Je n'arrive pas non plus à utiliser le fait que le spectre est strictement positif

par **Mike_51** » 06 Juin 2006, 17:12

pourquoi ne peut-il pas être négatif le spectre?

par **abel** » 06 Juin 2006, 17:14

Je n'en sais rien c'est dans l'énoncé donc ça doit avoir son importance...

par **yos** » 06 Juin 2006, 17:26

"C'est dans l'énoncé " mais tu l'avais pas dit il me semble.
Dans ce genre de truc, il faut définir le produit scalaire de R^n à l'aide de l'une des matrices (celle qui est définie>0, i.e. qui a des vp>0). Puis diagonaliser la seconde matrice ds un repère orthogonal pour la première. Du coup tu auras une base de R^n qui diagonalise les deux matrices en même temps.

par **abel** » 06 Juin 2006, 17:53

Merci bcp, je ne savais pas qu'on pouvais diagonaliser les 2 en meme temps. Je vais essayer de le faire en admettant ton résultat qui a l'air de tomber l'exo...
:++:

Sinon, c'est quoi la démarche pour prouver ceci ???

par **hans** » 06 Juin 2006, 18:04

Ce n'est pas exactement diagonaliser: si c'était le cas ca voudrait dire que toutes les matrices symétriques commutent entre elles:
c'est juste trouver

telle que

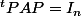
et

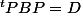
ou D est une matrice diagonale, P n'appartenant pas nécessairement au groupe orthogonal.
Les propriétés du déterminant font qu'on peut éliminer P pour conclure.

par **mln** » 06 Juin 2006, 18:10

Bonsoir,
Si on avait au moins une valeur propre négative, det(A)^(1/n) pourrait etre complexe.
Ca évite aussi de prendre B=-A où l'inégalité n'est pas toujours vraie.

par **abel** » 06 Juin 2006, 18:13

Je suis d'accord que ton résultat tombe l'exo mais le truc c'est que je ne vois pas d'où vient ce résultat...ni comment le démontrer...
Merci pour l'aide en tous cas :++:

par **hans** » 06 Juin 2006, 20:55

Revois la démonstration de la diagonalisabilité des matrices symétriques réelles en remplacant partout (|) par le produit scalaire associé à A et tu verras ca marche.

par **yos** » 06 Juin 2006, 21:12

hans a écrit:Ce n'est pas exactement diagonaliser: si c'était le cas ca voudrait dire que toutes les matrices symétriques commutent entre elles.

C'est juste, j'ai pas été très propre.

par **abel** » 07 Juin 2006, 11:27

On a démontré ce lemme ce matin pour corriger l'exo, et on a parlé un peu des matrices congruentes...Je comprend mieux maintenant.
:zen:

Oral type X-ENS

oral type X-ENS

Qui est en ligne