Sup et inf
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Jan 2012, 02:59
par Dinozzo13 » 28 Jan 2012, 02:59
Dinozzo13 a écrit:Voici mes résultats :

,
où
_{n\in\mathbb{N}^*)
et
_{n\in\mathbb{N}^*)
sont respectivement croissante et décroissante sur
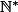
.
Et donc pour trouver l'inf et le sup, il faut évaluer suivant les valeurs de

et

: les signe de

et

?
Il y a un petit problème, on est en fait sur un sous-ensemble de
^2)
donc l'inf et le sup doivent être des couples.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 28 Jan 2012, 03:40
par Skullkid » 28 Jan 2012, 03:40
Non, l'ensemble qui t'intéresse est un sous-ensemble de R, pas de N². De plus, je ne crois pas que tu aies dans ton cours des théorèmes sur l'existence de bornes sup/inf sur N² (il faut de toute façon choisir une relation d'ordre sur N² pour que ça ait un sens).
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Jan 2012, 18:09
par Dinozzo13 » 28 Jan 2012, 18:09
Donc au final je trouve que l'inf est 1/2 et le sup vaut 1. Est-ce correct ?
Existe-t-il un relation pour trouver facilement ces inf et sup ?
Par exemple, est-ce que l'inf est le plus petit des réels 1/2 et (1+y)/(1+2y) ; le sup est le plus grand des réels (x+1)/(x+2) et 1 ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Jan 2012, 18:52
par Dinozzo13 » 28 Jan 2012, 18:52
Donc au final je trouve que l'inf est 1/2 et le sup vaut 1. Est-ce correct ?
Existe-t-il un relation pour trouver facilement ces inf et sup ?
Par exemple, est-ce que l'inf est le plus petit des réels 1/2 et (1+y)/(1+2y) ; le sup est le plus grand des réels (x+1)/(x+2) et 1 ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 28 Jan 2012, 21:34
par raito123 » 28 Jan 2012, 21:34
Oui c'est correct mais tu dois le démontrer ... pour ce ou tu montres que ces bornes sont atteintes ou bien qu'il existe une suite de (IN*)^2 telle que l'image de cette suite par ta fonction converge vers l'une des bornes ( la définition d'une borne quoi :) )
Les multiples ne doivent pas être utilisés sans nécessité
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Jan 2012, 21:54
par Dinozzo13 » 28 Jan 2012, 21:54
Eh bien c'est immédiat alors :
Si l'inf est le min de 1/2 et (1+y)/(1+2y) et le sup le max de (x+1)/(x+2) et 1 alors l'inf vaut 1/2 et le sup vaut 1.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Jan 2012, 00:01
par Doraki » 29 Jan 2012, 00:01
Dinozzo13 a écrit:Eh bien c'est immédiat alors :
Si l'inf est le min de 1/2 et (1+y)/(1+2y) et le sup le max de (x+1)/(x+2) et 1 alors l'inf vaut 1/2 et le sup vaut 1.
Si tu dis ça parceque t'as montré que pour tout x,y (x+1)/(x+2) >= (x+y)/(x+2y) >= (1+y)/(1+2y), alors ouais ça tient debout.

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 29 Jan 2012, 01:43
par alm » 29 Jan 2012, 01:43
Salut,
Voici une autre manière d'analyser ce problème :
Soit, pour tout

, l'ensemble :
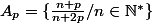
La fonction
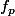
définie par
=\frac{x+p}{x+2p})
est croissante sur
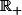
. Il en résulte que
=f_p(1)=\frac{p+1}{2p+1})
et
 = \lim_{n \to +\infty }f_p(n)=1)
.
.
On a :
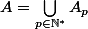
, donc

et si
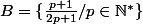
est l'ensemble de tous les plus petits éléménts des ensembles
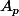
, il est aisé de voir que

.
Or

car la fonction

est décroissante sur
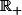
si bien que
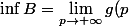= \frac 12)
, par suite , on a :

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Jan 2012, 12:44
par Dinozzo13 » 29 Jan 2012, 12:44
MOHAMED_AIT_LH a écrit: et si
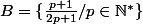
est l'ensemble de tous les plus petits éléménts des ensembles
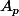
, il est aisé de voir que

.
Or

car la fonction

est décroissante sur
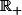
si bien que
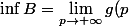= \frac 12)
, par suite , on a :

.
Salut !
Je comprends bien le début mais à partir d'ici, je ne comprends pas bien, pourrais-tu m'expliquer.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Jan 2012, 14:25
par Dinozzo13 » 29 Jan 2012, 14:25
Ah, je pe avoir compris, je vais faire de même avec le sup :++:
-
mathelot
 par mathelot » 29 Jan 2012, 14:31
par mathelot » 29 Jan 2012, 14:31
je suis assez d'accord avec tout ce qui a été écrit précédemment
simple et élégant:
en posant

, puis

on a juste à étudier les bornes des fonctions
=\frac{1+\alpha}{2 +\alpha})
et
=\frac{1+\alpha}{1 +2 \alpha})
sur


-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 29 Jan 2012, 19:28
par alm » 29 Jan 2012, 19:28
Salut
Dinozzo13 a écrit:.
Salut !
Je comprends bien le début mais à partir d'ici, je ne comprends pas bien, pourrais-tu m'expliquer.
l'ensemble

est la réunin des
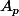
quand

décrit
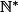
, donc la borne inférieur de

est égale à celle del'ensembles des inf des
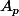 Plus comprendre miex on donne la démo dans le cas de deux parties de
Plus comprendre miex on donne la démo dans le cas de deux parties de 
:
Si

alors si

et

sont non vides et si

est minoré B et C sont minorées et on a :
=\inf(\inf(B),\inf(C)))
.
En effet si

est un minorant de A c'est bien aussi un minorant de B et de C , donc

et

sont minorées et

et

donc
 \quad \inf A \leq \inf( \inf B, \inf C))
Or si
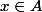
alors
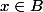
ou
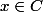
donc

ou

et comme
)
et de même
)
on a bien
)
par passage à l'inf on a donc
 \quad\inf A \geq \inf (\inf B, \inf C))
Conclusion : compte tenue de
)
et
)
on a
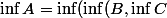)

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 29 Jan 2012, 19:31
par alm » 29 Jan 2012, 19:31
Dinozzo13 a écrit:Ah, je pe avoir compris, je vais faire de même avec le sup :++:
Oui! et c'est déjà fait en haut car l'ensemble des sup est un singletons : ça ne pose aucun problème ...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Jan 2012, 00:09
par Dinozzo13 » 30 Jan 2012, 00:09
D'ailleurs, je comprends pourquoi je ne voyais pas de borne sup, j'avais commis l'erreur de penser que
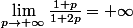
! :--:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
,
et
sont respectivement croissante et décroissante sur
.
et
: les signe de
et
?
