Sup et inf

[Dinozzo13]

Bonjour, je voudrais déterminer le sup et l'inf de l'ensemble suivant :
,
mais avec une méthode simple et élégante.
Merci d'avance pour vos réponses

[SphinxDeLOblast]

Bonjour, je voudrais déterminer le sup et l'inf de l'ensemble suivant :
,
mais avec une méthode simple et élégante.
Merci d'avance pour vos réponses

elegante j'en sais rien mais n'oubliez pas que N possede une relation d'ordre

[SphinxDeLOblast]

elegante j'en sais rien mais n'oubliez pas que N possede une relation d'ordre

n+p = 0 on ne pourra pas faire mieux dans la N

[Dinozzo13]

oups, oui j'ai oublié de préciser que .

N possède une relation d'ordre et alors ? (Je ne vois pas)

[Skullkid]

Salut, avant tout il est de bon ton de remarquer que ton ensemble est bel et bien borné, et on peut regarder si les majorant et minorant "intuitifs" sont, ou pas, des bornes sup/inf. Plus globalement, t'as un machin de deux variables (que tu peux d'ailleurs commencer par essayer de réécrire sous une forme plus simple) donc une première piste serait de regarder comment il se comporte quand tu fixes une variable et que fais bouger l'autre.

[raito123]

Salut,

Une solution pas élégante mais pas du tout est de déterminer les points critiques d'une fonction à deux variables :)

[Pythales]

Peut-être écrire que

[Dinozzo13]

Ah oui, pas bête. J'avais pensé au 2nd membre mais pas au 3e :++:

Je vais voir ce que ca donne.

[raito123]

Ah oui, pas bête. J'avais pensé au 2nd membre mais pas au 3e :++:

Je vais voir ce que ca donne.

ça marche très bien juste avec le second membre

[Dinozzo13]

A votre avis, j'hésite, vaut-il mieux étudier les fonctions définies sur par et ?
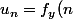Ou étudier leur suite asscociée ? A savoir et ?

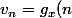[Skullkid]

As-tu essayé les approches que tu proposes ? Et as-tu cherché s'il y avait des bornes "évidentes" comme je te l'ai conseillé dans mon premier post ?

[Dinozzo13]

Voici mes résultats :
,
où et sont respectivement croissante et décroissante sur .
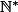
Et donc pour trouver l'inf et le sup, il faut évaluer suivant les valeurs de et : les signe de et ?

[Dinozzo13]

Voici mes résultats :
,
où et sont respectivement croissante et décroissante sur .
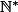
Et donc pour trouver l'inf et le sup, il faut évaluer suivant les valeurs de et : les signe de et ?

[Skullkid]

Juste avec une réécriture de la quantité de départ (comme celles que t'a proposés Pythales par exemple), à ton avis, quelles sont les bornes ?

[Dinozzo13]

Je pense que les bornes sont et .

[Skullkid]

Ok, donc maintenant que tu as des candidats, ça devrait pas être top dur de voir si ce sont les bons : si tu prouves que ce sont bien des majorants/minorants et que tu peux faire tendre (n+p)/(n+2p) vers eux, tu as gagné. L'analyse avec les fonctions et/ou la réécriture sert surtout à trouver des candidats plausibles.

[Dinozzo13]

Ben les limites en +\infty pour n et p donne bien ces deux nombre.
Mais quand je représente la surface représentative je trouve que l'inf est 1/2 mais qu'il n'y a pas de sup

[Skullkid]

Comment pourrait-il ne pas y avoir de sup ? C'est une partie bornée de R... Le problème vient sans doute du fait que la surface que tu as tracée représente , qui est un tout autre ensemble.

Edit : d'ailleurs non, même en étendant l'ensemble comme je l'ai fait il y a encore un sup... je vois pas d'où vient ton problème du coup.

[Dinozzo13]

Ben lors je ne vois quel pourrait être le sup.
Une piste ?

[Sa Majesté]

L'ensemble est majoré par 1.

D'autre part, si tu fixes p=1 par ex, tu obtiens , qui tend vers 1 quand n tend ver l'infini.
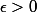
Dis autrement, si tu prend un tu peux trouver un n (fonction de ) tel que .
A toi de le montrer et de conclure.