Réciproque du TVI ?

[Nightmare]

Hello,

un beau cadeau de noël :

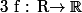
est telle que :

- L'image d'un segment est encore un segment ()
- Quel que soit x réel, la limite de toute suite convergente d'antécédents de x en est encore un antécédent.

Montrer que f est continue

:happy3:

[ffpower]

Niveau lycée? ( enfin, lycée+ :we: )

[Nightmare]

Oui, lycée+ :lol3:

[benekire2]

Salut !

Je ne comprends pas trop ta phrase : "- Quel que soit x réel, la limite de toute suite convergente d'antécédents de x en est encore un antécédent."

Parce que telle que je la comprends, si on prends f(x)=x pour x rationnel et f(x)=-x par x irrationnel , je crois que f vérifie le TVI et pourtant , une suite d'antécédents de 2 pour moi c'est 2;2;2;2....;2 qui converge vers ... 2 qui est bien un antécédent de 2 et pourtant le seul et unique point de continuité de f semble être 1/2 !

J'ai donc mal compris l'exercice :we:

[Nightmare]

Hello,

l'image d'un intervalle par ta fonction n'est pas du tout un intervalle !

Par exemple l'image de [0 ; 1] contient tous les rationnels entre 0 et 1 et tous les irrationnels entre 0 et -1, et tout ça ne forme pas du tout un intervalle !

La phrase plus mathématiquement dit que l'ensemble des antécédents de x est fermé. Un ensemble est dit fermé si toute suite convergente de ses éléments a sa limite qui est encore dans l'ensemble (d'où le mot "fermé"), ou plus visuellement, un ensemble est fermé s'il contient ses "extrémités" (qui sont exactement les limites de ses suites...).

[benekire2]

Hello,

l'image d'un intervalle par ta fonction n'est pas du tout un intervalle !

Euh... oui tu as raison :ptdr:

Bon, je vais voir ce que je peut faire alors :zen:

[benekire2]

Bon, l'idée c'est de montrer que pour un intervalle ouvert ]a,b[ f(]a,b[)=I où I est encore un intervalle. Je verrais cela cette après midi, mais ça m'a l'air faisable en utilisant la deuxième donnée !

[Nightmare]

Je ne te suis pas, on veut montrer que f est continue, pas qu'elle vérifie le TVI !

[benekire2]

Je ne te suis pas, on veut montrer que f est continue, pas qu'elle vérifie le TVI !

Mince oui Heureusement que t'es là !

[ffpower]

Commence par écrire la définition de continuité, ça peut aider :)

[benekire2]

Commence par écrire la définition de continuité, ça peut aider

T'en fais pas j'ai quand même une idée de preuve :

soit x fixé, y=f(x) je prends un intervalle I=]a,b[ contenant y et puis c'est pas très dur de trouver un intervalle J tel que f(J) inclus dans I et contenant y. Ce qui permet de conclure.

Bon, faut que je réécrive ce merdier proprement mais l'idée y est amha.

[Nightmare]

Un peu de détails bene?

[benekire2]

Salut nightmare !

Quand c'est si gentillement demandé... je vais faire l'effort :we: :

(En fait il s'agissait d'une "idée")

Donc l'idée c'est que la définition de la continuité c'est : quel que soit la taille de l'intervalle I=]a,b[ contenant y on peut trouver un intervalle J contenant x tel que

Je n'est fait que la reprendre , et donc suffit de trouver le J en question ... comme ceci :

On peut trouver un intervalle J contenant x et où il n'y a pas d'antécédents de a et b et par construction f(J) est inclus dans I puisque comme f(J) est un intervalle, s'il contenait zb alors il contiendrait b. Bon, en fait l'idée de prendre J sans qu'il y ait des antécédents de a et b dedans vient ... de la fin de la justification , j'y avais pas trop pensé avant :ptdr:

[ffpower]

Bien joué :we:

[Nightmare]

C'est limpide ! Et si on remplace x réel par x rationnel ?

[benekire2]

C'est limpide ! Et si on remplace x réel par x rationnel ?

Re,

Bon, je me casse les dents a installer un foutu logiciel , mais a mon avis soit on conclu par densité soit on ne conclu pas par densité, a voir :lol3: (bon, je n'apporte rien ok)

[ffpower]

La première piste m'a l'air pas mal :lol3:

[benekire2]

La première piste m'a l'air pas mal :lol3:

En fait ce que je voulais dire c'est soit on montre que c'est vrai par densité, soit on montre que c'est pas vrai par densité, je suis assez convaincu en voyant la tête du truc que on a "que la densité dans le sac" même si c'est peut être faux ... en tout cas j'ai toujours rien foutu depuis ...