Exercice sur les suites

[Megane86000]

C'est vrai que vu comme ça c'est beaucoup plus simple ! On n'utilise que des propriétés déjà connues et je me suis aperçue que la propriété que j'utilisais était justement la propriété à démontrer à l'exo 3 ...

D'ailleurs pour l'exo 3 j'ai remarqué une faute j'ai écrit "une limite de rationnels" au lieu de "une suite de rationnels" ;)

J'aimerais quand même arriver à faire le 3 seule mais j'ai déjà une petite hésitation :hum:

Ils définissent a^x comme la limite de a^qn quand qn tend vers x. Il faut ensuite démontrer que cette propriété reste valable pour : a^x * a^y = a^(x+y) ce qui revient à démontrer que a^qn * q^pn = a^(pn+qn). Or nous avons déjà utilisé cette propriété sans la démontrer donc ?! Est-ce que ça fausserait nos démonstrations des exercices 2 et 1 ou ce n'est pas la même :hein:

Encore une fois merci !

[Megane86000]

Salut !

Un ami qui n'est pas du tout sûr de sa réponse a essayé de faire et le 3 et est arrivé à faire le cas de la multiplication en 1 ligne et celui de l'exposant lui aurait pris 3 pages il m'a dit, il faudrait utiliser des sous-suites selon lui. C'est une bonne piste ou il s'est carrément gouré ? ^^

Merci

[Megane86000]

Bonjour,

Désolée d'encore vous déranger mais j'ai bossé sur l'exercice 3, j'arrive à obtenir ce qu'il faut mais je ne sais pas du tout si ma méthode est exacte :hum:

Pour le premier : Si a^x est la limite de a^qn, on peut dire que la limite de a^pn est a^y.

On sait que lim (a^pn*a^qn) = lim (a^pn+qn) = a^x+y
Par les regles de calculs on sait que la limite d un produit est egal au produit des limites donc ; lim (a^pn*a^qn) = lim a^pn * lim a^qn = a^x * a^y ==> a^x*a^y = a^x+y


Pour le deuxieme ; si a^x est la limite de a^qn et a^y la limite de a^pn alors x est la limite de qn et y la limite de pn.

Donc lim (a^qn)^pn = (a^x)^y
lim (a^qn)^pn = lim (a^qn*pn) = a^xy

Donc (a^x)^y = a^xy

[Ben314]

Pour le produit, il n'y a pas de problème : tu utilise le résultat disant que le produit de deux suites convergentes est lui même convergent et que la limite est le produit des limites : cela n'a rien à voir avec les puissances et donc peut tout à fait être supposé "déjà connu".

Pour les puissances, par contre, je suis à peu prés sûr que ton raisonnement utilise au fond le fait que, si Un->L et Vn->L' alors (Un)^(Vn)->L^L' et ça tu ne peut pas dire que c'est "déja connu" avant d'avoir définis ce qu'est une puissance.

A mon avis, la première chose à démontrer, c'est que, pour tout quotient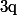 , on a , c'est à dire (toujours avec la définition) que où est une suite de quotient qui tend vers (donc tend vers ) :
Si (a,b entiers naturels), le fait connu qu'un produit de suites convergentes tendent vers le produit des limites implique que ce qui prouve le résultat.

Ensuite, utilise la monotonie de la fonction (qui découle immédiatement de la monotonie de déjà montrée) pour conclure.

[Megane86000]

Merci énormément :)

Je me suis rendu compte que j'avais faux car j'écris que lim (a^qn)^pn = (lim a^qn)^lim pn , ce qui est faux par exemple pour (1+1/n)^n = e et non à 1