Existe-t-il une application
Longueur d'un graphe
19 messages
- Page 1 sur 1
Longueur d'un graphe
par Zweig » 07 Sep 2010, 23:00
Salut,
Existe-t-il une application
, continue et strictement croissante de sorte que la longueur de son graphe vaille 2 ?
Existe-t-il une application
par gigamesh » 07 Sep 2010, 23:11
Hum...
Intuitivement, non.
Si la fonction est continue, je dirais bien qu'on peut l'approcher par une ligne brisée.
Un coup de Pythagore et une identité remarquable et ça devrait le faire.
bof, ça passe pas à la limite...
Bon je vais y réfléchir en dormant !
Intuitivement, non.
Si la fonction est continue, je dirais bien qu'on peut l'approcher par une ligne brisée.
Un coup de Pythagore et une identité remarquable et ça devrait le faire.
bof, ça passe pas à la limite...
Bon je vais y réfléchir en dormant !
par Ericovitchi » 08 Sep 2010, 08:47
Intuitivement on sens que non car même en la faisant passer par 0,0 et 1,1 et en la rapprochant le plus possible de (1,0) on voit que l'on ne pourra pas dépasser la longueur des 2 cotés du carré donc 2. Restes à démontrer ça rigoureusement. Travailler sur 
avec des considérations variationnelles, ça semble un peu ésotérique !
par windows7 » 08 Sep 2010, 11:23
tu parlais de segment de droite alors ?
si oui : ca se montre tres bien par reccurence en fonction du nombre de sommet
exemple le seul cas possible pour n=3 c'est la solution proposé par je c plus qui.
si c'est pas vrai pour un rang n suppose que c'est vrai pour n+1
et soit malin.
sinon +1 pour doraki : c'est quoi la longueur ?
si oui : ca se montre tres bien par reccurence en fonction du nombre de sommet
exemple le seul cas possible pour n=3 c'est la solution proposé par je c plus qui.
si c'est pas vrai pour un rang n suppose que c'est vrai pour n+1
et soit malin.
sinon +1 pour doraki : c'est quoi la longueur ?
par Matt_01 » 12 Sep 2010, 18:49
En utilisant la densité des fonctions affines par morceaux ca doit passer non ?
par Imod » 13 Sep 2010, 11:17
Il me semble qu'on peut parler de longueur pour toute courbe à variation bornée ce qui est le cas de toute fonction monotone .
On doit pouvoir se passer de la dérivée !
Imod
On doit pouvoir se passer de la dérivée !
Imod
par Doraki » 13 Sep 2010, 12:01
J'ai bien l'impression que la réponse est oui.
En tout cas si on accepte les fonctions croissantes non strictement, un truc comme l'escalier de cantor devrait marcher.
En tout cas si on accepte les fonctions croissantes non strictement, un truc comme l'escalier de cantor devrait marcher.
par Ben314 » 13 Sep 2010, 12:15
Salut,
On peut toujours définir la longueur d'une courbe paramétrée
(euclidien) comme la borne supérieure (éventuellement infinie) des -\gamma(t_{k-1})||)
où 
décrit l'ensemble de toutes les subdivisions possibles de [a,b].
Dans le cas où
est de classe 
, c'est un exercice "classique" de montrer que la longueur est ||dt)
Bien évidement, on peut appliquer cette définition pour calculer la longueur du graphe de toute fonction
.
Il est assez facile de montrer que, si la fonction est monotone, la longueur du graphe est majorée par 2.
Il est trivial de produire un exemple de fonction croissante (au sens large) et non continue dont la longueur du graphe vaut 2.
Il est nettement moins trivial d'en produire un où f est croissante (au sens large) et continue (le seul qui me vient à l'esprit est "l'escalier du diable").
Il n'est pas non plus trivial de produire un exemple avec f strictement croissante mais non continue (prendre une fonction faisant des "sauts" en tout points d'un ensemble dense de [0,1] et, évidement tels que la somme des sauts fasse 1)
Quand à la question initiale, à savoir de produire un exemple avec f strictement croissante ET continue, je voterais bien que c'est impossible mais j'ai pas trop cherché de preuve... (je chercherais quand j'aurais un peu de temps...)
Edit (du fait que j'avais pas lu le post de Doraki) : sauf erreur,
l'escalier de cantor = escalier du diable = fonction singulière de Lebesgue = ... ???
et il me semble (à vérifier) que la première publi sur le sujet n'est... ni de Cantor, ni de Lebesgue...
Edit 2 (aprés 8h de cours donc....) :
je me demande si, en prenant la fonction de répartition d'une proba sur [0,1] sans partie continue par rapport à la mesure de lebesgue mais telle qu'aucun point n'ait un poid non nul, ça ne fonctionnerais pas...
Par exemple, en prenant 1/2<p<1, q=1-p puis
mu([0,1/2])=p ; mu([1/2,1])=q ;
mu([0,1/4])=p² ; mu([1/4,1/2])=mu([1/2,3/4]=pq ; mu([3/4,1]=q² ;
mu([0,1/8])=p^3 ; mu([1/8,1/4])=mu([1/4,3/8]=mu([1/2,5/8]=p²q ; mu([3/8,1/2]=mu([5/4,3/4]=mu([3/4,7/8]=pq² ; mu([7/8,1]=q^3 ;
etc...
On peut toujours définir la longueur d'une courbe paramétrée
Dans le cas où
Bien évidement, on peut appliquer cette définition pour calculer la longueur du graphe de toute fonction
Il est assez facile de montrer que, si la fonction est monotone, la longueur du graphe est majorée par 2.
Il est trivial de produire un exemple de fonction croissante (au sens large) et non continue dont la longueur du graphe vaut 2.
Il est nettement moins trivial d'en produire un où f est croissante (au sens large) et continue (le seul qui me vient à l'esprit est "l'escalier du diable").
Il n'est pas non plus trivial de produire un exemple avec f strictement croissante mais non continue (prendre une fonction faisant des "sauts" en tout points d'un ensemble dense de [0,1] et, évidement tels que la somme des sauts fasse 1)
Quand à la question initiale, à savoir de produire un exemple avec f strictement croissante ET continue, je voterais bien que c'est impossible mais j'ai pas trop cherché de preuve... (je chercherais quand j'aurais un peu de temps...)
Edit (du fait que j'avais pas lu le post de Doraki) : sauf erreur,
l'escalier de cantor = escalier du diable = fonction singulière de Lebesgue = ... ???
et il me semble (à vérifier) que la première publi sur le sujet n'est... ni de Cantor, ni de Lebesgue...
Edit 2 (aprés 8h de cours donc....) :
je me demande si, en prenant la fonction de répartition d'une proba sur [0,1] sans partie continue par rapport à la mesure de lebesgue mais telle qu'aucun point n'ait un poid non nul, ça ne fonctionnerais pas...
Par exemple, en prenant 1/2<p<1, q=1-p puis
mu([0,1/2])=p ; mu([1/2,1])=q ;
mu([0,1/4])=p² ; mu([1/4,1/2])=mu([1/2,3/4]=pq ; mu([3/4,1]=q² ;
mu([0,1/8])=p^3 ; mu([1/8,1/4])=mu([1/4,3/8]=mu([1/2,5/8]=p²q ; mu([3/8,1/2]=mu([5/4,3/4]=mu([3/4,7/8]=pq² ; mu([7/8,1]=q^3 ;
etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 07 Oct 2010, 11:29
Je remonte le topic du fait que ça fait un moment que ça me tarabusquait de savoir si l'exemple que je donne marche ou pas (mais il fallait trouver le temps...) :
On fixe
, 
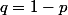et on construit les fonctions 
telles que :
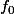est l'identité, puis, récursivement, 
est affine sur chaque intervalle 
(
) avec une pente 
et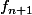 
s'obtient en partant de la même valeur en 
puis en prenant une pente de 
sur la première moitié de l'intervalle et une pente de 
sur la deuxième moitié (ce qui donne bien la même valeur que celle de en 
)
Il est clair que les fonctions sont continues et strictement croissantes est quelles convergent uniformément vers une fonction f qui est continue et strictement croissante.
Vu la construction, la longueur
du graphe de 
est minorée par les longueurs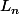 
des graphe des .
En regardant les pentes des différents segments composant, on voit que :
^2+(2^{-n})^2})
et donc, que si on fixe un
(par exemple la moyenne) on a :
Or, en utilisant la convergence des lois binomiales vers la loie normale, on voit que chacune des deux sommes tend vers 1 lorsque
tend vers 
: le graphe de est bien de longueur 
.
On fixe
Il est clair que les fonctions
Vu la construction, la longueur
En regardant les pentes des différents segments composant
et donc, que si on fixe un
Or, en utilisant la convergence des lois binomiales vers la loie normale, on voit que chacune des deux sommes tend vers 1 lorsque
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par ffpower » 07 Oct 2010, 11:55
On avait aussi réfléchi a ton idée avec un ami, et on a obtenu que ce que tu disait était génériquement vrai : n'importe quelle fonction continue monotone de dérivée nulle pp marche. L'idée est de "presque recouvrir" l'ensemble des points ou f' différent de 0 ( autrement dit le support de la mesure singuliere df dont f est la fonction de répartition ) par une suite finie d'intervalles disjoints [ak,bk], 1
Après ta démo a évidemment plus sa place en section olympiades ( si ce n'est qu'il faudrait prouver la convergence vers la loi normale de maniere élémentaire, mais je suppose que ca doit pouvoir se faire )
Après ta démo a évidemment plus sa place en section olympiades ( si ce n'est qu'il faudrait prouver la convergence vers la loi normale de maniere élémentaire, mais je suppose que ca doit pouvoir se faire )
par Ben314 » 07 Oct 2010, 14:54
Ben justement, un petit "défi" (sic)
Qui peut trouver la preuve la plus élémentaire possible du fait que, pour
fixés,
^{n-k}<br />\ =\ 0)
(évidement j'ai pas de réponse et c'est trés nettement moins fort que la convergence d'une binomiale vers une loie normale)
Qui peut trouver la preuve la plus élémentaire possible du fait que, pour
(évidement j'ai pas de réponse et c'est trés nettement moins fort que la convergence d'une binomiale vers une loie normale)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par ffpower » 07 Oct 2010, 21:26
Me suis pris au jeu :we:
En constatant que pour^2)
, on a
^{n-k}\leq S=\frac{1}{n^2(p-\lambda)^2}\sum_{k=0}^{n}(k-np)^2{n\choose k}p^k(1-p)^{n-k})
Or :
^2{n\choose k}=k(k-1){n\choose k}-(2np-1)k{n\choose k}+n^2p^2{n\choose k}=n(n-1){n-2\choose k-2}-(2np-1)n{n-1\choose k-1}+n^2p^2{n\choose k})
Ce qui permet de découper S en 3 sommes et d'utiliser la formule du binome à chacune d'entre elles, pour obtenir, à des termes de bord près qui tendent vers 0 :
^2}[n(n-1)p^2-(2np-1)np+n^2p^2])
, ce qui quand n tend vers l'infini tend vers }(p^2-2p^2+p^2)=0)
En constatant que pour
Or :
Ce qui permet de découper S en 3 sommes et d'utiliser la formule du binome à chacune d'entre elles, pour obtenir, à des termes de bord près qui tendent vers 0 :
par Ben314 » 07 Oct 2010, 21:32
Trés joli (et trés élémentaire)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par benekire2 » 08 Oct 2010, 16:23
magnifique !
Je me demande même d'où te vient l'idée ffpower ... très jolies astuces d'écriture !
Je me demande même d'où te vient l'idée ffpower ... très jolies astuces d'écriture !
par ffpower » 09 Oct 2010, 13:08
Ah mais tu m'oblige à dévoiler les coulisses là, ça va être moins impressionnant du coup 
Bon ok tant pis j'explique. En fait j'ai essentiellement essayer de reprendre la preuve probabiliste du truc et de la réécrire sans proba. L'idée probabiliste est la suivante :)
étant une suite de variables aléatoire indépendante dans {0,1} avec 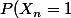=p)
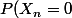, =1-p)
( suite de pile/face avec une piece biaisée ), la quantité exprimée par Ben est précisément \leq \frac{Var(X)}{\delta^2}))
. C'est précisément ce que j'ai utilisé pour ma 1ere inégalité, mais en virant tout ce qui parle de proba. Après la 2eme étape consiste à dire que pour des variables aléatoires indépendantes, variance de la somme=somme des variances, ie que =Var(Y_1)+\cdots+Var(Y_n))
, et les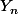 
ayant même variance ( à savoir )
), ça donne finalement =np(1-p))
et donc \leq \frac{p(1-p)}{n(\lambda-p)^2})
ce qui montre que ca tend bien vers 0. Mais pour cette 2eme étape, je n'ai malheureusement pas réussi à la réécrire clairement sans parler de probas, donc du coup à partir de là j'ai poursuivi le calcul à la main..
Bon ok tant pis j'explique. En fait j'ai essentiellement essayer de reprendre la preuve probabiliste du truc et de la réécrire sans proba. L'idée probabiliste est la suivante :
par benekire2 » 28 Oct 2010, 09:35
Salut ff, j'avais pas eu le temps de tout lire alors j'avais pas répondu , mais bravo :we: C'est beau !
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :