Limite/Continuite
24 messages
- Page 1 sur 2 - 1, 2
Limite/Continuite
Bonsoir,
Je considère la fonction f(x) défini par:
f(x) = 5 si x=0
f(x) = |x| si x != 0
Quelle est la limite de f(x) en 0 ?
Je pense que c'est 0 même si f(0)=5 mais j'aimerais avoir une confirmation.
Merci
Je considère la fonction f(x) défini par:
f(x) = 5 si x=0
f(x) = |x| si x != 0
Quelle est la limite de f(x) en 0 ?
Je pense que c'est 0 même si f(0)=5 mais j'aimerais avoir une confirmation.
Merci
Je dis ça car pour moi , la limite de f(x) en a est L si :
- limite a gauche de a de f(x) = L
- limite a droite de a de f(x) = L
Alors faut-il a ces deux conditions ajouter : - f(a)= L ?
Si oui alors f(x) continue en a est totalement équivalente a f(x) admet une limite finie en a non ? et donc on aurait deux expressions qui disent exactement la même chose ?
- limite a gauche de a de f(x) = L
- limite a droite de a de f(x) = L
Alors faut-il a ces deux conditions ajouter : - f(a)= L ?
Si oui alors f(x) continue en a est totalement équivalente a f(x) admet une limite finie en a non ? et donc on aurait deux expressions qui disent exactement la même chose ?
Perso, il y a une chose dont je suis sûr, c'est que les deux seule réponses possibles sont :
1) Il n'y a pas de limite en 0
2) Il y a une limite en 0 qui vaut 0.
Aprés, tout dépend de la définition que l'on prend de limite (i.e. enlève t'on systématiquement le cas x=xo lorsque x->xo ?).
Dans le cadre "trés général" de la topologie... générale :doh: , il me semble que quasi tout les auteurs gardent le point xo.
Par contre, au lycée, j'ai l'impression qu'il y a beaucoup moins unanimité sur la définition.
Si tu as des doutes, tu écrit lim f(x)=0 en écrivant évidement en dessous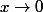 mais en écrivant aussi (encore en dessous ou à coté)
mais en écrivant aussi (encore en dessous ou à coté) 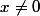 .
.
Comme ça il ne peut pas y avoir d'ambiguïté sur ce que cela signifie.
1) Il n'y a pas de limite en 0
2) Il y a une limite en 0 qui vaut 0.
Aprés, tout dépend de la définition que l'on prend de limite (i.e. enlève t'on systématiquement le cas x=xo lorsque x->xo ?).
Dans le cadre "trés général" de la topologie... générale :doh: , il me semble que quasi tout les auteurs gardent le point xo.
Par contre, au lycée, j'ai l'impression qu'il y a beaucoup moins unanimité sur la définition.
Si tu as des doutes, tu écrit lim f(x)=0 en écrivant évidement en dessous
Comme ça il ne peut pas y avoir d'ambiguïté sur ce que cela signifie.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si l'on prend la définition suivante:
f(x) admet une limite L en p si
pour tout réel ;) > 0 il existe un réel ;) > 0 tel que pour tout x dans D tel que |x - p| < ;), on ait |f(x) - L| < ;).
En prenant cette définition alors la limite de f(x) en p est égale a L si:
-f(p)=L
-limite a droite de p (x != p ) =L
-limite a gauche de p (x != p) =L
Mais alors si f(x) n'est pas défini en p cela nempêche pas d'avoir une limite en p non ?
f(x) admet une limite L en p si
pour tout réel ;) > 0 il existe un réel ;) > 0 tel que pour tout x dans D tel que |x - p| < ;), on ait |f(x) - L| < ;).
En prenant cette définition alors la limite de f(x) en p est égale a L si:
-f(p)=L
-limite a droite de p (x != p ) =L
-limite a gauche de p (x != p) =L
Mais alors si f(x) n'est pas défini en p cela nempêche pas d'avoir une limite en p non ?
Qmath a écrit:Je pense que c'est plutôt ça car je viens de lire dans un manuel MPSI que si f(x) est defini en a et que f(x) admet une limite finie en a alors celle-ci est égale a f(a) .
A mon avis, c'est mieux de prendre ça comme définition et de rajouter le
Edit : je suis allé regardé sur Wikipédia : http://fr.wikipedia.org/wiki/Limite_(math%C3%A9matiques)
Evidement les deux définitions sont données (avec le vocable "limite épointé" dans le cas ou on enlève la valeur de xo) et, via la note (2) en bas de page, il est précisé que :
2.C'est cette définition (non "épointée") de limite d'une fonction qui est désormais en vigueur en France (programmes - plus ou moins précis - régulièrement publiés au Bulletin Officiel) dans l'enseignement secondaire et les classes préparatoires [archive], supplantant la définition historique de Weierstrass qui correspond à celle appelée dès lors "limite épointée" ou "limite par valeurs différentes" ([1]). Mais dans les universités françaises (et dans les autres pays [2]), la définition "historique" reste parfois celle enseignée : cf par exemple Mathématiques L1, Cours complet avec 1000 tests et exercices corrigés sous la direction de J.-P. Marco et L. Lazzarini (2007) Pearson, ISBN 9782744072581, p. 691-692, ou encore Mathématiques. Tout-en-un pour la Licence. Niveau L1 sous la direction de J.-P. Ramis et A. Warusfel (2006) Dunod, ISBN 210049614X, p. 588.
A noter aussi que le même article de Wiki. mais en anglais : http://en.wikipedia.org/wiki/Limit_(mathematics) donne comme unique définition celle "épointé" (donc pas la même qu'en france) et qu'il en est de même pour l'article plus détaillé : http://en.wikipedia.org/wiki/Limit_of_a_function
(j'ai pas regardé le même article dans toutes les langues pour faire des statistiques...)
Conclusion : C'est bien le bordel et effectivement, la définition donnée au Lycée (en particulier en prépa)... dépend des bouquins...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Faudra donc se renseigner en début dannée a chaque fois ...
Par contre je ne vois pas quels avantages a la définition épointée par rapport a l'historique qui on fait qu'on commence de plus en plus a l'adopter. Peut être seulement pour qu'on ait pas deux notions qui sont strictement identique (continue en un point/ admet une limite finie en un point)
Merci Ben et Dinozzo
Par contre je ne vois pas quels avantages a la définition épointée par rapport a l'historique qui on fait qu'on commence de plus en plus a l'adopter. Peut être seulement pour qu'on ait pas deux notions qui sont strictement identique (continue en un point/ admet une limite finie en un point)
Merci Ben et Dinozzo
Ben314 a écrit:Conclusion : C'est bien le bordel et effectivement, la définition donnée au Lycée (en particulier en prépa)... dépend des bouquins...
Tout à fait d'accord.
Et malheureusement pas seulement dans ce cas-ci.
Même si beaucoup ont souvent soutenu que ce n'était pas vrai et que tous les matheux du monde étaient tous d'accord sur les définitions.
:zen:
Attention, la définition "historique" de Weierstrass, c'est celle "épointée" donc pas la même que celle sensée être la "définition française" selon le ministère.Qmath a écrit:Faudra donc se renseigner en début dannée a chaque fois ...
Par contre je ne vois pas quels avantages a la définition épointée par rapport a l'historique qui on fait qu'on commence de plus en plus a l'adopter. Peut être seulement pour qu'on ait pas deux notions qui sont strictement identique (continue en un point/ admet une limite finie en un point)
Comme tu le fait remarquer, les deux définitions conduisent heureusement à la même notion de continuité et de dérivabilité donc cela ne change pas bien grand chose pour la suite. Pour la continuité, avec la "définition française" on peut même écrire simplement "f continue en xo ssi elle admet une limite en xo" mais ça a pas bien d'interêt.
Aprés, le seul cas où les définitions diffèrent est celui que tu présente dans ton premier post où f(x) admet une limite lorsque x tend vers xo en restant différent de xo mais que cette limite n'est pas égale à f(xo).
Enfin, je pense que, dans 99% des exos, ça change rien du fait que, quasi systématiquement, si la fonction f est déjà définie en xo, l'exercice demandera "d'étudier la continuité de f en xo".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Concernant le fait qu'il y a d'autres définitions qui diffèrent d'un bouquin à l'autre : O.K.Black Jack a écrit:Tout à fait d'accord.
Et malheureusement pas seulement dans ce cas-ci.
MAIS, systématiquement, cela signifie que les théories que l'on bati avec les deux définitions (différentes) sont les mêmes.
Or, si on prenait (tout à fait par hasard et par exemple... :zen:) comme définition d'une fonction T-périodique que c'est une fonction telle que T est la plus petite période, alors toute la théorie tombe à l'eau du fait que l'ensemble des fonctions T-périodiques ne serait plus un espace vectoriel !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Concernant le fait qu'il y a d'autres définitions qui diffèrent d'un bouquin à l'autre : O.K.
MAIS, systématiquement, cela signifie que les théories que l'on bati avec les deux définitions (différentes) sont les mêmes.
Or, si on prenait (tout à fait par hasard et par exemple... :zen:) comme définition d'une fonction T-périodique que c'est une fonction telle que T est la plus petite période, alors toute la théorie tombe à l'eau du fait que l'ensemble des fonctions T-périodiques ne serait plus un espace vectoriel !
Sans relancer le débat.
Tu penses vraiment que cela empêche qu'il existe plusieurs définitions pour "la période", il suffit de chercher un peu sur le net pour avoir la réponse ... qui ne fait aucun doute. ?
Je n'attends pas de réponse. :we:
:zen:
Black Jack a écrit:Sans relancer le débat.
On a presque envie d'y croire.
PS : A priori tu ne sais de toute façon pas ce qu'est la notion de débat, puisque tu ne sembles en aucun cas tenir compte des arguments des autres.
PS2 : Concernant le sujet initial du topic, Cf une discussion identique [url="http://maths-forum.com/showthread.php?t=99790"]ici[/url]
Black Jack a écrit:Tu penses vraiment que cela empêche qu'il existe plusieurs définitions pour "la période"
oui.
Ce qui ne fait aussi aucun doute, c'est qu'en cherchant sur le net, tu trouvera surement quelque part que :Black Jack a écrit:...il suffit de chercher un peu sur le net pour avoir la réponse ... qui ne fait aucun doute. ?
1) La terre est plate
2) Elle a été crée il y a 4000 ans et, si on trouve des fossiles, c'est uniquement parce que dieu les y a mis pour amuser les humains.
3) Le réchaufment climatique et le trou dans la couche d'ozone n'ont absolument rien à voir avec l'activité humaine.
4) Il est logique que dans une sociétée ou 10% de la population cherche du travail que l'on demande à ceux qui ont un travail de le garder plus longtemps.
etc,etc,etc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Attention Ben, le 4 ne peut être absurde puisqu'il dépend de la logique appliquée, donc du but recherché...
Économiser de l'argent sur le dos du pékin de base : Réussi.
Faire travailler les seniors : Échec.
-> 50% de réussite. Le président ayant été élu avec 53%, cela ne fait que 3% de perdu.
(les maths et la politique, c'est quelque-chose quand même)
Économiser de l'argent sur le dos du pékin de base : Réussi.
Faire travailler les seniors : Échec.
-> 50% de réussite. Le président ayant été élu avec 53%, cela ne fait que 3% de perdu.
(les maths et la politique, c'est quelque-chose quand même)
ffpower a écrit:J'aime ta maniere de progresser discretement de trivialités vers tes opinions politiques :we:
ATTENTION, je n'ai absolument jamais affirmé, (mais vraiment jamais du tout), ni même sous entendu que ces quatres phrases étaient absurdes : vous voyez vraiment le mal partout... :triste:Finrod a écrit:Attention Ben, le 4 ne peut être absurde puisqu'il dépend de la logique appliquée, donc du but recherché...
Je voulais simplement dire que, sur le Net, on trouve TOUT... et son contraire...
A chacun de décider, pour chacune des quatres affirmations, si elle fait partie du 'TOUT' ou... de son contraire... :marteau:
P.S. pour ffpower : j'ai longtemps hésité quand à la liste d'exemple que j'allais mettre. Celle là m'a parru... satisfaisante...
P.S.2 (plus sérieux) : je viens juste de réagir qu'avec la définition "historique" (voisinages épointés), si on prend les deux fonctions R->R suivantes :
a) f(x)=1 pour tout réel x
b) g(x)=2 pour tout réel x sauf pour x=1 où g(x)=g(1)=3.
alors :
1) f(x) tend vers 1 lorsque x tend vers 0.
2) g(x) tend vers 2 lorsque x tend vers 1.
3) gof(x) tend vers 3 lorsque x tend vers 0.
C'est tout de même un peu ennuyeux il me semble...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En faisant quelques exemples je me rend compte que la definition historique est dans certains cas plus adaptee.
Soit la fonction f(x):
f(x)=1 pour tout x != 0
f(x)=2 pour x=0
Soit la suite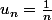
quand n ---> +oo , ----> 1) donc
donc ) tend vers la limite de f(x) en 0 (si on prend la definition historique)
tend vers la limite de f(x) en 0 (si on prend la definition historique)
Je pense que ceci est vrai pour la mojorite des suites ( que j'ai rencontre bien sur) c'est a dire des suites qui admettent des limites mais qui "ne l'atteingnent pas" a la diffrence des suites du genre .
.
Qu'en pensez vous ?
Soit la fonction f(x):
f(x)=1 pour tout x != 0
f(x)=2 pour x=0
Soit la suite
quand n ---> +oo ,
Je pense que ceci est vrai pour la mojorite des suites ( que j'ai rencontre bien sur) c'est a dire des suites qui admettent des limites mais qui "ne l'atteingnent pas" a la diffrence des suites du genre
Qu'en pensez vous ?
Effectivement, comme la définition "historique" donne des fois des limites alors que dans le même cas la "définition française" dit qu'il n'y a pas de limite, ça peut être utile dans certains exercices.
Mais, comme le montre l'exemple de mon dernier post, il semble quand même que la "définition française" soit plus adaptée pour écrire des "théorème généraux" :
Par exemple dans le théorème :
Si Un->L lorsque n->oo et que f(x)->L' lorsque x->L alors f(Un)->L' lorsque n->oo
ben si on prend la définition "historique", il faut rajouter que :
à condition que, à partir d'un certain rang, tout les termes de la suite (Un) soient distincts de L
et ça "ralonge" le théorème...
Mais, comme le montre l'exemple de mon dernier post, il semble quand même que la "définition française" soit plus adaptée pour écrire des "théorème généraux" :
Par exemple dans le théorème :
Si Un->L lorsque n->oo et que f(x)->L' lorsque x->L alors f(Un)->L' lorsque n->oo
ben si on prend la définition "historique", il faut rajouter que :
à condition que, à partir d'un certain rang, tout les termes de la suite (Un) soient distincts de L
et ça "ralonge" le théorème...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
