Bonjour à tous.
Voici l'énoncé de mon problème : Un équipement électronique est composé de deux modules M1 et M2. On pose les évènements :
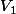
= "M1 est en panne"
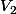
= "M2 est en panne"
Il est prévu de mettre l'équipement en service à une date future, que nous noterons t = 0. Les évènements
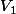
et
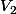
seront réalisés
certainement, mais à des dates inconnues comprises entre 0 et +;).
On pose les variables aléatoires :

: représentant la durée écoulée avant réalisation de
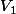

: représentant la durée écoulée avant réalisation de
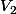
Les fonctions
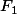
(t) et
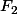
(t) donnant les probabilités de réalisation des évènements "

< t" et "

< t" sont supposées connues. Elles sont croissantes et tendent vers 1, ce sont donc les fonctions de répartition des lois attachées aux variables

et

. Pour fixer les idées, disons que ce sont des lois exponentielles de paramètres
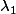
et
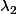
:
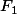
(t) = 1 - exp(-
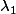
* t)
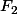
(t) = 1 - exp(-
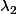
* t)
On suppose que les modules M1 et M2 participent à une certaine "fonction matérielle", laquelle devient définitivement défaillante si M1 tombe en panne (même si M2 tombe en panne plus tard), et qui devient définitivement bonne si M2 tombe en panne (même si M1 tombe en panne plus tard).
Voici ma question : Quelle est la probabilité
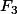
(t) pour que la fonction matérielle soit en panne à l'instant t (c'est à dire soit tombée en panne entre 0 et t) ?
On note que
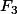
est une fonction croissante, mais qu'elle tend nécessairement vers une limite inférieure à 1 à cause du module M2, ce n'est donc pas une fonction de répartition.
Merci de votre aide,
Pierre
