Polaire et cartésien
38 messages
- Page 2 sur 2 - 1, 2
Il faut que tu fasse un schéma pour éviter de te tromper de signe.
Il faut faire gaffe avec la touche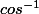 de la calculatrice.
de la calculatrice.
Garde les fractions et les racines, tu dois normalement connaitre par coeur les valeurs de cosinus et sinus 0, Pi/6, Pi/4, Pi/3, Pi/2 et savoir retrouver les autres grâce aux règles que vérifies ces deux fonctions.
Une fois que tu a trouvé , tu cherche un
, tu cherche un  qui vérifie
qui vérifie  = \frac{x}{\rho}) et
et  = \frac{y}{\rho})
Il faut faire gaffe avec la touche
Garde les fractions et les racines, tu dois normalement connaitre par coeur les valeurs de cosinus et sinus 0, Pi/6, Pi/4, Pi/3, Pi/2 et savoir retrouver les autres grâce aux règles que vérifies ces deux fonctions.
Une fois que tu a trouvé
"et donc sa c'est la réponse a la premiere qiestion ? "
Ce n'est pas évident pour tout le monde ! à méditer !
On doit chercher l'angle à l'aide du CERCLE TRIGONOMETRIQUE
Il faut revoir les bases je te donne un autre exemple:

Arnaud-29-31 a écrit:Oui doncce qui donne
mais il y'a aussi la 2ème équation qu'il ne faut pas oublier, à savoir
et qui confirme que
Ce n'est pas évident pour tout le monde ! à méditer !
On doit chercher l'angle à l'aide du CERCLE TRIGONOMETRIQUE
Il faut revoir les bases je te donne un autre exemple:

Aha = )
Donc :
1) on sait d'apres le cours que les coordonnées polaire d'un point A dans le plan cartésien est sous la forme A [ r, phi ] avec r = OA donc A a pour coordonnées polaires [OA, phi]
On cherche OA
OM= racine((xA-X0)² + (yA-Y0)²)
= racine((1/2-0)² + ( -1/2-0)²)
= racine (1/2)² + (-1/2)²
= 1/racine(2)
= racine(2)/2
Donc A [racine(2)/2), phi]
On cherche phi
cos(phi) = x/r = x/OA = (1/2)/(racine(2)2)= ? ...
Donc :
1) on sait d'apres le cours que les coordonnées polaire d'un point A dans le plan cartésien est sous la forme A [ r, phi ] avec r = OA donc A a pour coordonnées polaires [OA, phi]
On cherche OA
OM= racine((xA-X0)² + (yA-Y0)²)
= racine((1/2-0)² + ( -1/2-0)²)
= racine (1/2)² + (-1/2)²
= 1/racine(2)
= racine(2)/2
Donc A [racine(2)/2), phi]
On cherche phi
cos(phi) = x/r = x/OA = (1/2)/(racine(2)2)= ? ...
38 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 104 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :




