Bonjour, aujourd'hui je vous propose un exercice issu d'un bac C assez cool, alors accrochez-vous bien, c'est long :ptdr: . Bonne chance :+++:
@Benekire : Ca devrait te faire plaisir : il est à la fois
sympa et
long ^^.
On notera

l'ensemble des entiers naturels,

l'ensemble des entiers naturels non nuls,

l'ensemble des entiers naturels privé des nombres
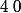
et
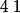
.
Partie AOn considère les suites
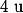
et
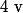
définies sur

par

et

et, pour tout

, élément de

:

\times n})
a) Trouver deux réels
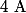
et
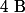
tels que, pour tout

, élément de

:
n}=\frac{A}{n-1}+\frac{B}{n})
En déduire que pour tout

, élément de

:

b) Montrer que la suite
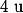
est croissante, que, pour tout élément de

:

, et que la suite
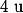
est majorée.
Partie BOn rappelle que, si

est un nombre complexe différent de
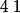
et

élément de

, alors :

1°) Soit

un élément de [0,\pi]; on pose pour

élément de

:
=\sum_{k=1}^n \cos kt)
et
=\sum_{k=1}^n \sin kt)
a) Calculer le nombre complexe :
+iS_n(t))
.
En déduire que, si
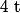
est un élément de

:
=\frac{\sin \frac{nt}{2} \cos \frac{n+1}{2}t }{\sin \frac{t}{2}})
et si
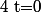
alors
=n)
.
b) L'application

de

dans

est-elle continue sur

?
2°) Vérifier que pour tout
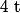
, élément de

:
=\frac{\sin \frac{2n+1}{2}t}{\sin \frac{t}{2}})
et montrer que l'application de

dans
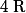
, qui à
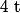
associe
)
, peut-être prolongée en une fonction

continue sur

.
3°) Montrer que pour tout

, élément de

:
\cos nt dt=\frac{1}{n^2})
.
En déduire que :
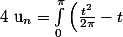 C_n(t) dt)
.
4°) Vérifier que :
dt=\frac{\pi^2}{6})
et que, pour tout

, élément de

:
g_n(t)dt)
.
Partie COn considère la fonction numérique

définie sur

par
=2)
et pour tout
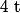
, élément de

:
=\frac{t- \frac{t^2}{2\pi}}{\sin \frac{\pi}{2}})
.
1°) Montrer que

est continue sur

; en déduire l'exitence d'un réel

tel que, pour tout
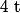
, élément de

:
 \le M)
2°) Soit
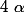
un réel fixé tel que

.
a) Montrer que, pour tout

, élément de

:
\sin \frac{2n+1}{2} t dt \right|\le \alpha M)
.
b) Montrer que

est dérivable sur

et que la fonction dérivée est continue sur ce segment. En déduire l'existence d'un réel

tel que, pour tout
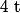
, élément de

:
|\le M')
.
c) on pose, pour tout

, élément de

:
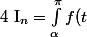\sin \frac{2n+1}{2} tdt)
.
Montrer, en utilisant une intégration par partie, que :

.
3°) Déduire de la question 2°) que :
 =0)
Et voilà, ouf, c'est fini ! j'ai plus de doigts ! :ptdr:
