Bonjour,
du point de vue de la topologie et du calcul différentiel , un tore est le
produit cartésien de deux cercles
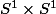
Ce qui correspond au paramètrage intuitif (solide de révolution)
Le tore est bien une variété analytique (sans trop s'avancer, le produit de deux variétés analytiques doit l'être aussi)
Une variété analytique, c'est quand les changements de cartes
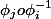
sont beaucoup plus que différentiables, sont holomorphes.
Par exemple, en 4 variables réelles
)
les changements de cartes sont en fait holomorphes des variables
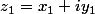
et
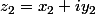
réfléchissons,
il doit être possible de voir les fonctions définies sur
un tore
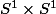
comme des fonctions de

définies sur un quadrillage, à double périodicité, et "passant au quotient":
pour le motif de base du quadrillage, il faut que la fonction de
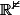
à quotienter prennent les mêmes valeurs sur les bords opposés.
Il ya un critère pour savoir si une fonction de
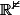
, donc de deux variables réelles (x,y) est holomorphe.
Elle doit être dans le noyau de l'application linéaire

et ses séries de Taylor locales de deux variables (x,y) sont en fait des séries
de l'unique variable z=x+iy
maintenant, j'ai envie de dire (grosse bêtise ?)
il n'y aurait-il pas uniquement les fonctions constantes comme fonctions holomorphes sur le tore ?? comme quotient de fonctions holomorphes bornées sur

??
sur la sphère, c'est en quelles dimensions ?
il existe des fonctions holomorphes de n variables

qui vérifient des formules de Cauchy à n variables.