Normalisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 10:54
par barbu23 » 14 Jan 2010, 10:54
Bonsoir à tous : :happy3:
J'ai un peu de mal à comprendre le théorème suivant et son intêret :
Soit

un corps et

une

algèbre de type fini, intègre.

, algebriquement independants sur

tels que

soit entier sur

.
Est ce que vous avez un exemple concret qui résume ce que dit ce théorème ?
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Jan 2010, 13:24
par Nightmare » 14 Jan 2010, 13:24
Salut,
je comprends pas la définition de A... C'est une flèche ou une algèbre?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 13:34
par barbu23 » 14 Jan 2010, 13:34
Désolé, j'ai recopié un peu plus vite le texte : :happy3:
 $)
est une

algèbre ! :happy3:
Merci Nightmare ! :happy3:
Au faut, as tu un exemple d'application de ce theorème ? :happy3:
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Jan 2010, 13:53
par Nightmare » 14 Jan 2010, 13:53
Dire que A est entière sur k[x1,...,xn] revient simplement à dire que tout élément de A s'annule en un certain polynôme de k[x1,...,xn] !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 14:51
par barbu23 » 14 Jan 2010, 14:51
ça veut dire que un element de

s'écrit de la manière suivante :
 $)
avec

, et donc, d'après ce que tu dis, il existe un certain polynome de

:

qui annule
 $)
, i.e :
, ... , P(x_1,...,x_n))=0 $)
, c'est ça ? :hum:
MErci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Jan 2010, 14:57
par Nightmare » 14 Jan 2010, 14:57
Non, ce que je dis c'est qu'un élément a de A est entier sur k[x1,...,xn] s'il existe un polynôme P à coef dans k[x1,...,xn] tel que P(a)=0 ! En clair ça correspond au terme "algébrique" lorsque A est un corps.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 17:31
par barbu23 » 14 Jan 2010, 17:31
Merci Nightmare, c'est clair maintenant ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 18:13
par barbu23 » 14 Jan 2010, 18:13
Bonsoir : :happy3:
svp, quelqu'un peut -t-il m'expliquer ce qu'on entend par corps parfait , en theorie des corps ? :happy3:
Un exemple concret qui illustre clairement ce fait svp ? :happy3:
Merci d'avance ! :happy3:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Jan 2010, 20:11
par abcd22 » 14 Jan 2010, 20:11
Nightmare a écrit:Non, ce que je dis c'est qu'un élément a de A est entier sur k[x1,...,xn] s'il existe un polynôme P à coef dans k[x1,...,xn] tel que P(a)=0 !
Et le coefficient dominant de P doit être 1 (c'est une condition importante pour montrer l'équivalence entre « x est fini sur A » et « A[x] est une A-algèbre finie »).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Jan 2010, 21:14
par barbu23 » 14 Jan 2010, 21:14
barbu23 a écrit:Bonsoir : :happy3:
svp, quelqu'un peut -t-il m'expliquer ce qu'on entend par corps parfait , en theorie des corps ? :happy3:
Un exemple concret qui illustre clairement ce fait svp ? :happy3:
Merci d'avance ! :happy3:
svp, une petite reponse à ce message ! :happy3:
Par contre, je ne comprends pas ce que tu veux dire par

fini dans

abcd ! :happy3:
MErci d'avance ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Jan 2010, 22:30
par Ben314 » 14 Jan 2010, 22:30
Salut barbu,
Comme j'avais oublié ce qu'est un corp parfait, j'ai tapé "corps parfait" sous google et, aprés avoir maté toute les photos pas ininteressantes sur le sujet (ce qui explique le temps mis pour ma réponse... :zen:) je tombe (évidement) là dessus, avec théorème et contre exemple...
http://fr.wikipedia.org/wiki/Corps_parfaitQui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Jan 2010, 22:53
par ffpower » 14 Jan 2010, 22:53
Mdr Ben
Ca me rappelle la premiere fois ou j ai innocemment cherché des ressources Latex
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Jan 2010, 12:32
par barbu23 » 15 Jan 2010, 12:32
Ok ! merci Ben ! :happy3:
Bref, un corps parfait est celui dont toutes ses extensions algebriques sont separables ! cette definition est la base de demosntration du theorème de l'element primitif ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Jan 2010, 12:37
par barbu23 » 15 Jan 2010, 12:37
Bonjour à tous : :happy3:
Je cherche un exemple d'application de ce theorème, car je n'arrive pas à comprendre certains passages techniques de l'enoncé suivant :
Proposition :Soit
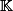
un corps parfait.
Soit
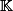
sa cloture algebrique.
Soit

irréductible dans

telle que :
 = Y^{n} + a_{n-1}(X) Y^{n-1} + ... + a_{0}(X) $$)
avec :
) \leq n-i $)
.
Soit :
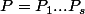
la factorisation en irréductibles de

dans

.
Soit :
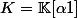
l'extension de

engendré par
les coefficients de

.
Dans ce cas :
 = Y^{m} + b_{m-1}(\alpha_{i} , X) Y^{m-1} + ... + b_{0}(\alpha_{i} , X) $$)
où :

est irréductible dans

et

et
 \leq m-k $)
et

sont les conjugués de

.
Question : $)
Que veut dire :

sont les conjugués de

?
 $)
Comment calcule -t-on les

dans :
 = Y^{m} + b_{m-1}(\alpha_{i} , X) Y^{m-1} + ... + b_{0}(\alpha_{i} , X) $$)
Bref, comment obtient - -ton à l'aide d'un exemple concret l'expression :
 = Y^{m} + b_{m-1}(\alpha_{i} , X) Y^{m-1} + ... + b_{0}(\alpha_{i} , X) $$)
?
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Jan 2010, 12:56
par barbu23 » 15 Jan 2010, 12:56
Pour la première question :
Ce que je connais est que les conjugués sont les racines d'un polynomes dans un corps de decompsitiion maximale ! Ce corps de decomposition est le plus souvent,normal et séparable, ça je connais ! mais ici c'est different , on est dans une algèbre de polynomes à plusieurs indeterminés ! :happy3:
Merci de votre aide ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Jan 2010, 14:06
par barbu23 » 15 Jan 2010, 14:06
svp, un petit coup de main ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Jan 2010, 14:09
par Ben314 » 15 Jan 2010, 14:09
Pour ta première question,

est dans l'extention
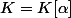
de
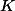
donc la notion de "conjugués de

" est la notion usuelle de conjugué (celle dont tu parle)
Pour la deuxième question, je ne sais pas trop, je n'ais pas une grande culture sur le sujet.
Un exemple simple qui me vient tout de suite à l'esprit est celui de
=Y^n-X^n)
vu comme polynôme de

et qui est trés simple à factoriser dans

...
Si ça peut t'aider à comprendre le théorème...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités