N!
Olympiades mathématiques, énigmes et défis
-
Anonyme
 par Anonyme » 12 Mar 2006, 02:32
par Anonyme » 12 Mar 2006, 02:32
prove que n! < (n/2)^n et n > 1
merci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Mar 2006, 10:21
par yos » 12 Mar 2006, 10:21
Mais pour n>5, c'est une simple récurrence (utilisant la minoration
^n>2)
qui se fait avec Bernoulli par exemple).
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 16 Mar 2006, 17:18
par isortoq » 16 Mar 2006, 17:18
On a une majoration valable pour tout n, mais un peu moins bonne, en utilisant la concavité de la fonction ln :
n!<[(n+1)/2]^n
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 16 Mar 2006, 18:18
par isortoq » 16 Mar 2006, 18:18
yos a écrit:Mais pour n>5, c'est une simple récurrence (utilisant la minoration
^n>2)
qui se fait avec Bernoulli par exemple).
Bernoulli ?
En fait, y'a plus simple il me semble puisque pour x>0 on a : (1+x)^n>1+nx
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Mar 2006, 18:39
par yos » 16 Mar 2006, 18:39
isortoq a écrit:Bernoulli ?
En fait, y'a plus simple il me semble puisque pour x>0 on a : (1+x)^n>1+nx
C'est ce qu'on appelle l'inégalité de Bernoulli!!
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 16 Mar 2006, 19:59
par isortoq » 16 Mar 2006, 19:59
yos a écrit:C'est ce qu'on appelle l'inégalité de Bernoulli!!
AH BON !... décidément toutes les inégalités ont un nom célèbre...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Mar 2006, 20:21
par yos » 16 Mar 2006, 20:21
Il y a aussi plus simple : (n+1)^n est le nombre de façons d'extraire n boules d'une urne qui en renferme n+1 (tirage avec remise) et 2n^n est le nombre de ces tirages pour lesquels une boule donnée a été tirée au plus une fois.
D'où
^n\geq 2n^n)
: c'est l'inégalité cherchée.
-
megrabi
- Messages: 5
- Enregistré le: 16 Mar 2006, 20:24
-
 par megrabi » 16 Mar 2006, 20:27
par megrabi » 16 Mar 2006, 20:27
Ah , je vois qu il ya bcp de solutions.
mais peut quelqu un faisez cette exercise:
soit a ,b et c des entiers strictement positifs tels que :
a/b+b/c+c/a est un entier
montrer que abc est un cube.
merci
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Aoû 2006, 13:03
par aviateurpilot » 15 Aoû 2006, 13:03
Soit p un nombre premier,et
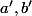
et
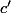
les valuations p-adiques
de
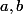
et

. On veut montrer que a'+b'+c' est un multiple de 3.
on a
+(b'-c')+(c'-a')= 0)
Il en résulte que lun au moins des trois entiers

et

est négatif. Si aucun
nest strictement négatif, cest que

et

est bien muliple de 3. Sinon, pour que
)
>ou =0 ,
on suppose que

et

et

dans ce cas on aura
=min(a'-b',b'-c',c'-a'))
et puisque
+(b'-c')+(c'-a')=0)
on va trouver un nombre a'+b'+c'=3b' (multiple de 3)
donc si p divise abc
)
est divisible par 3
donc
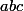
est un cube
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
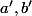 et
et 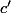 les valuations p-adiques
les valuations p-adiques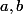 et
et  . On veut montrer que a'+b'+c' est un multiple de 3.
. On veut montrer que a'+b'+c' est un multiple de 3.+(b'-c')+(c'-a')= 0)
 et
et  est négatif. Si aucun
est négatif. Si aucun et
et  est bien muliple de 3. Sinon, pour que
est bien muliple de 3. Sinon, pour que ) >ou =0 ,
>ou =0 ,  et
et  et
et 
=min(a'-b',b'-c',c'-a'))
+(b'-c')+(c'-a')=0) on va trouver un nombre a'+b'+c'=3b' (multiple de 3)
on va trouver un nombre a'+b'+c'=3b' (multiple de 3)) est divisible par 3
est divisible par 3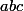 est un cube
est un cube