Variation niveau seconde
44 messages
- Page 2 sur 3 - 1, 2, 3
bonjour
donc pour
g-->racine x²+1 dg R+
pour (a,b) E dg ag(b)-g(a)=(racine b²+1)-(racine a²+1)
= racine b²+1-a²-1
=racine b²-a²
=racine (b-a)(b+a)
racine (b-a)>0 et racine (b+a)>0 donc g(b)-g(a)>0 alors g est strict croissant sur R+
je pense que c est bon
par contre je seche pour
h-->1/x²+1 normalement dh R* mais x²+1 etant tjr positif ???
pr tt (a,b) E dh
h(b)-h(a)=1/b²+1 - 1/a²+1
=b²-a²/(b²+1)(a²+1) là je bloque pour simplifier le denominateur
voila
donc pour
g-->racine x²+1 dg R+
pour (a,b) E dg ag(b)-g(a)=(racine b²+1)-(racine a²+1)
= racine b²+1-a²-1
=racine b²-a²
=racine (b-a)(b+a)
racine (b-a)>0 et racine (b+a)>0 donc g(b)-g(a)>0 alors g est strict croissant sur R+
je pense que c est bon
par contre je seche pour
h-->1/x²+1 normalement dh R* mais x²+1 etant tjr positif ???
pr tt (a,b) E dh
h(b)-h(a)=1/b²+1 - 1/a²+1
=b²-a²/(b²+1)(a²+1) là je bloque pour simplifier le denominateur
voila
Heuuuuu,
non, là c'est "pas trés bon" car n'est pas égal à
n'est pas égal à  .
.
Si tu veut faire dans cet exercice "tout pareil" que dans les autre, je pense que tu est obligé d'utiliser une "astuce" consistant à écrire :
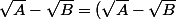(\sqrt{A}+\sqrt{B})\over \sqrt{A}+\sqrt{B}}={A-B\over \sqrt{A}+\sqrt{B}}) (au numérateur, c'est une identité remarquable)
(au numérateur, c'est une identité remarquable)
sauf que je ne suis pas sûr du tout que ce soit la méthode "adaptée à ton niveau"
Pour le deuxième exemple, le dénominateur est déjà "trés simple" (on voit bien que c'est toujours positif) donc cela ne sert à rien de le tripatouiller.
Par contre, pour le numérateur, il faudrait peut être l'écrire autrement pour bien voir s'il est positif ou négatif.
non, là c'est "pas trés bon" car
Si tu veut faire dans cet exercice "tout pareil" que dans les autre, je pense que tu est obligé d'utiliser une "astuce" consistant à écrire :
sauf que je ne suis pas sûr du tout que ce soit la méthode "adaptée à ton niveau"
Pour le deuxième exemple, le dénominateur est déjà "trés simple" (on voit bien que c'est toujours positif) donc cela ne sert à rien de le tripatouiller.
Par contre, pour le numérateur, il faudrait peut être l'écrire autrement pour bien voir s'il est positif ou négatif.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
si c est une astuce qu on a vu mais on y pense pas tt le temps seul le prof y pense pas nous !!!!
donc pour
g-->racine x²+1 dg R+
pour (a,b) E dg ag(b)-g(a)=(racine b²+1)-(racine a²+1)
= (racinede b²+1 -racinede a²+1)(racinede b²+1 +racinede a²+1)/racinede b²+1 +racinede a²+1
=b²+1-a²+1/racinede b²+1 +racinede a²+1
=(b+a)(b-a)/racinede b²+1 +racinede a²+1
(b+a)>0 et (b-a)>0 et racinede b²+1>0 et racinede a²+1 >0 sur R+
donc g(b)-g(a)>0 alors g est strict croissant sur R+
c est bon la ou pas
donc pour
g-->racine x²+1 dg R+
pour (a,b) E dg ag(b)-g(a)=(racine b²+1)-(racine a²+1)
= (racinede b²+1 -racinede a²+1)(racinede b²+1 +racinede a²+1)/racinede b²+1 +racinede a²+1
=b²+1-a²+1/racinede b²+1 +racinede a²+1
=(b+a)(b-a)/racinede b²+1 +racinede a²+1
(b+a)>0 et (b-a)>0 et racinede b²+1>0 et racinede a²+1 >0 sur R+
donc g(b)-g(a)>0 alors g est strict croissant sur R+
c est bon la ou pas
par contre je suis embeté pour
h-->1/x²+1 normalement dh R*
pr tt (a,b) E dh
h(b)-h(a)=1/b²+1 - 1/a²+1
=b²-a²/(b²+1)(a²+1)
=(b-a)(b+a)/(b²+1)(a²+1)
donc bref tt est positif et h(b)>h(a) donc h est strict croissant mais j ai du mal a me representer graphiquement un hyperbole (ma calcu a planter) croissante le carre me joue t il des tours
voila
h-->1/x²+1 normalement dh R*
pr tt (a,b) E dh
h(b)-h(a)=1/b²+1 - 1/a²+1
=b²-a²/(b²+1)(a²+1)
=(b-a)(b+a)/(b²+1)(a²+1)
donc bref tt est positif et h(b)>h(a) donc h est strict croissant mais j ai du mal a me representer graphiquement un hyperbole (ma calcu a planter) croissante le carre me joue t il des tours
voila
Bonjour je donne bénévolement des cours de maths. Si tu veux que je t'aide il te suffit de m'envoyer tes sujets par mails via ton scan en précisant :
- Ta classe
- Les questions que tu ne comprend pas
à l'adresse suivante maths.free@gmail.com
A bientot.
- Ta classe
- Les questions que tu ne comprend pas
à l'adresse suivante maths.free@gmail.com
A bientot.
vivi c'est bien 1/(x²+1)
exacte sinon !!!
=(a-b)(a+b)/(b²+1)(a²+1)
a-b<0 a+b>0 les autres termes positif
si je fais un tableau de signes h(b)-h(a) <0 et h strict decroissant sur R* en meme temps le domaine de def pourquoi il serait R* vu que x²+1 est tjr >0
et j arrive pas a me la representer c penible
exacte sinon !!!
=(a-b)(a+b)/(b²+1)(a²+1)
a-b<0 a+b>0 les autres termes positif
si je fais un tableau de signes h(b)-h(a) <0 et h strict decroissant sur R* en meme temps le domaine de def pourquoi il serait R* vu que x²+1 est tjr >0
et j arrive pas a me la representer c penible
44 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
