Borne de Cauchy
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 19 Sep 2009, 14:21
par jeje56 » 19 Sep 2009, 14:21
Bonjour,
On définit la borne de Cauchy p(f) du polynôme de C[X] de degré n
=\sum_{k=0}^{n}a_kX^k)
comme étant l'unique racine réelle strictement positive de l'équation :

On pose
=a_nX^n+\sum_{k=0}^{n-2}a_kX^k) MQ
MQ \le p(f))
: Je ne vois pas comment répondre... J'ai essayé par l'absurde : supposons p(f1)>p(f), alors :
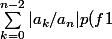^k>\sum_{k=0}^{n-1}|a_k/a_n|p(f)^k)
C'est-à-dire :
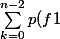^k>\sum_{k=0}^{n-1}p(f)^k)
Je ne vois pas la contradiction...
Merci de votre aide !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 19 Sep 2009, 16:13
par jeje56 » 19 Sep 2009, 16:13
Personne ?...
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 19 Sep 2009, 21:18
par jeje56 » 19 Sep 2009, 21:18
Merci Angélique pour ta réponse ! En effet je travaille sur l'épreuve de Capes 09 !
p(f) étant la borne de Cauchy de f(X) et p(f1) celle de f1(X)...
Angélique_64 a écrit:donc si x0 est la borne de Cauchy de f, on a 2x0^n= f(x0)
Je ne vois vraiment pas d'où cela vient...
Merci bcp !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 20 Sep 2009, 09:16
par jeje56 » 20 Sep 2009, 09:16
Oui, c'est bon je vois... Merci :-) Je regarde la suite...
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 20 Sep 2009, 09:26
par jeje56 » 20 Sep 2009, 09:26
Angélique, as tu l'épreuve sous la main ?
Je suis à la question 3.2) de la partie B : MQ si z est racine de f alors
)
... As-tu un indice ?
Merci à toi !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 20 Sep 2009, 14:32
par jeje56 » 20 Sep 2009, 14:32
Lol, je veux bien ! ;-)
Edit : je répondais au post précédent... ;-)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 20 Sep 2009, 14:40
par jeje56 » 20 Sep 2009, 14:40
Angélique_64 a écrit:si z est racine,
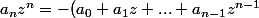)
Si tu prends le module de chaque coté, et tu majores le membre de droite, tu obtiens une inégalité qui permettrait d'affirmer que |z| est plus petit que la borne de Cauchy (toujours grâce à la croissance que tu as démontrée avant )
Merci bcp, c'est clair !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 20 Sep 2009, 14:54
par jeje56 » 20 Sep 2009, 14:54
Je bute aussi sur le 2.1) de la partie B :
Je pense qu'il faut MQ

est la borne de Cauchy de
)
: ainsi zéta racine de F(X) implique zéta racine de
)
d'où l'inégalité demandée...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités