Problème de logique-reformulation lié au TVI

[lucie68]

Bonjour à tous !

Alors voilà, je prépare l'oral du CAPES, et j'ai un petit souci concernant une leçon.
Dans le théorème des valeurs intermédiaires, on impose à la fonction d'être continue.
je dis alors que cette hypothèse est indispensable, en effet, j'ai exhibé un exemple qui montre que une fonction qui n'est pas continue peut ne pas vérifier le thérème des valeurs intermédiaires.
Il peut en effet exister des y n'ayant pas d'antécédents.

Néanmoins, après je dis que la continuité est suffisante mais n'est pas nécessaire.
En effet, là encore j'ai exhibé un exemple d'une fonction qui n'est pas continue mais qui vérifie le TVI quand même.

Alors en relisant ce que j'avais écrit, j'avais un peu l'impression que c'est en contradiction.
Le terme 'hypothèse indispensable' n'est pas judicieux, si?
Et y a t-il un moyen simple par une phrase d'expliquer ce que je viens de dire?

Merci beaucoup pour votre aide !!

[uztop]

Bonjour,

si la fonction n'est pas continue, tu ne peux pas conclure avec le TVI (comme tu l'as montre avec ton contre exemple).
Ca n'empeche pas que tu puisse trouver des fonctions non continues qui verifient quand meme le TVI. Je ne pense pas que c'est une bonne idee de montrer cet exmple de fonction non continue qui verifie le TVI; ca risque de perturber les eleves dans le cadre d'un vrai cours.

Edit: la continuite est bien une hypothese indispensable pour conclure en utilisant le theoreme

[amstramgram]

salut!

Etant donné que le TVI est énoncé pour des fonctions continues, je pense que ce n'est pas très judicieux de donner un exemple de fonction non continue qui vérifie le TVI. C'était quoi d'ailleurs cette fonction ?

[Nightmare]

La continuité est une hypothèse trop forte pour le TVI. Darboux a démontré par exemple qu'admettre des primitives suffisait pour vérifier le TVI, je ne sais pas s'il y a équivalence (je ne pense pas)

Cela dit dans le secondaire ce n'est pas vraiment utile de parler de cela.

[Doraki]

C'est une hypothèse suffisante et non nécessaire.
Le théorème dit qu'il n'y a pas de fonction qui soit continue et qui ne vérifie pas le TVI,
mais il peut toujours exister les 3 autres sortes de fonctions :
- continue, qui vérifie le TVI
- non continue, qui ne vérifie pas le TVI
- non continue, qui vérifie le TVI.

amstramgram, un exemple de telle fonction :
Si x est dans [0;1], je regarde un développement en base 4 de x,
S'il y a un nombre infini de chiffres 0 ou 3 dans le développement, je prends f(x) = x.
Sinon, je retire tout ce qui se trouve jusqu'au dernier chiffre 0 ou 3, il reste alors une suite de chiffres 1 et 2. Je remplace les 2 par des 0, et je prends f(x) = le réel dont le développement binaire est cette suite de chiffres.

f est une fonction de [0;1] dans [0;1], telle que pour tout ouvert U de [0;1], f(U) = [0;1] : Toutes les valeurs possibles sont atteintes sur tous les intervalles ouverts, donc elle vérifie le TVI.

[busard_des_roseaux]

Bonjour,

as tu des souçis avec l'implication ?

si implique (est vraie)

alors
si A (la prémisse est vraie)
par modus ponens , B est vraie (la conclusion).

Içi,
si f est continue sur [a;b] alors f vérifie le TVI.

si f n'est pas continue sur [a;b], il n'y a pas de règle générale.

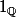l'indicatrice des rationnels ne vérifie pas le TVI.

Il me semble qu'il y a un théorème dû à Darboux qui indique
que si f est une fonction dérivée g' d'une fonction g, elle vérifie le TVI

la fonction vérifie le TVI.

On peut construire une fonction très pathologique qui vérifie le TVI
,en considérant par exemple une bijection ensembliste de [0;1]
sur [0;1]

[Nightmare]

Pour me répondre je suis quasiment sûr que le théorème de Darboux est une équivalence, il me semble qu'on peut construire des fonctions pathologiques continues nulles part mais vérifiant le TVI.

[lucie68]

OK merci beaucoup à tous !!
J'ai bien les idées au clair la dessus maintenant !
Merci :)

[ffpower]

Pour me répondre je suis quasiment sûr que le théorème de Darboux est une équivalence, il me semble qu'on peut construire des fonctions pathologiques continues nulles part mais vérifiant le TVI.

Tu veux dire que c est pas une équivalance plutot non? :we:

[Nightmare]

Oui, plutôt :mur:

[amstramgram]

merci doraki pour l'exemple... c'est sacrément tordu et j'étais loin d'imaginer quelque chose comme ça... :doh:

[uztop]

oui enfin, on peut aussi trouver moins tordu. La fonction de Doraki n'est continue nulle part; on peut aussi prendre une fonction qui n'est discontinue que en quelques points:
f(x)=x sur [0;1], sauf en deux points f(1/4)=3/4 et f(3/4)=1/4
prend bien toutes les valeurs entre 0 et 1 mais n'est pas continue sur l'intervalle

[Doraki]

Oui mais cette fonction ne vérifie pas le TVI.

Y'avait aussi le f(x) = sin(1/x) de busard en prenant f(0) au choix dans [-1,1].
C'est moins pathologique, c'est sur.

Et je crois que c'est l'exemple le plus simple qu'on puisse trouver.

[uztop]

oui effectivement, mon exemple n'est pas bon: il faut pouvoir choisir les valeurs m et n qu'on veut, dans mon cas je considere necessairement les valeurs 0 et 1.
J'aime bien l'exemple avec sin(1/x) :)
Enfin de toutes facons, je ne pense pas du tout que ca soit une bonne idee de sortir ce genre d'exemples dans un cours sur le TVI.

[Nightmare]

Désolé Doraki, je n'avais pas vu que tu avais déjà exhibé une fonction nulle part continue vérifiant le TVI avant de poster mon message.

Ce qui me turlupine quand même c'est qu'on a toujours pas à l'heure actuelle de CNS pour qu'une fonction vérifie le TVI. (D'ailleurs on ne devrait pas parler du TVI mais de la propriété des valeurs intermédiaires, le TVI étant le théorème qui stipule qu'une fonction continue vérifie cette propriété justement.)