Somme des termes consécutifs d'une suite.

[anto17]

Bonjour à tous,
j'ai un problème pour calculer la somme des termes consécutifs d'une suite qui ne semble ni arithmétique ni géométrique...
Voici le problème :

f est la fonction polynôme .
On note S=1+2+...+n et P=1²+2²+...+n²

1) f(x)= 3x²+3x+1

En remplaçant successivement x par 1; 2;...;n, démontrez que :

f(1)+f(2)+...+f(n) = = 3P + 3S + n

Merci beaucoup. :happy2:

[Ericovitchi]

Oui qu'est-ce qui te parait compliqué ?

Ecris f(1)+f(2)+...+f(n), est-ce que tu es arrivé à montrer que c'est 3P + 3S + n ? C'est assez simple

Après l'astuce est d'utiliser la forme pour f(x)
Ecris f(1)+f(2)+...+f(n) est-ce que les termes ne se simplifient pas ? Que reste t-il ?

[anto17]

Ce qui me paraît compliqué est que je ne sais pas comment exprimer la somme des termes consécutifs de f.

[Ericovitchi]

f(1) =
f(2) =
f(3) =
---------------------
f(n) =

Additionnes toutes ces équations de chaque coté du signe égal
Tu trouves f(1)+f(2)+....+f(n) = ??? en faisant apparaître P et S évidemment

[anto17]

Mon problème est que je ne sais pas exprimer la somme P ou f vu que ce ne sont des suites ni géométriques ni arithmétiques.

[Ericovitchi]

On ne t'a pas demandé de calculer P ou S, on t'a demandé de montrer que

Cela dit si tout à l'heure tu veux que je te montre comment on calcule P et S, c'est tout à fait possible.

Mais pourquoi ne suis tu pas la méthode que je t'ai donné.
Additionnes membre à membre chaque ligne, on trouve :
(car il y a n 1)

Maintenant essayes de montrer que c'est aussi égal à en utilisant la forme

[anto17]

Ah !!!! D'accord j'ai pas besoin de calculer ces sommes (pas impossible ?).
Maintenant le reste a l'air beaucoup plus dur.
Je ne vois pas comment le dernier terme peut être 1 avec des cubes.
Merci beaucoup.

[Ericovitchi]

Ca n'est pas plus dur.
écris pareil :
f(1) =
f(2) =
f(3) =
---------------------
f(n) =

Additionnes toutes ces équations membre à membre, qu'est-ce qu'il se passe ? et qu'est-ce qui reste des deux cotés ?

[anto17]

En fait la fin de l'exercice consite à trouver P en fonction de n.
J'ai réussi à le faire !!
Il ne me reste qu'à prouver que
Et là je dois avouer que je sèche.
Aucune formule de la somme de suites ne peut s'appliquer vu que ce n'est ni une fonction géométrique ni une fonction arithmétique.
Meme avec ta méthode (Ericovitchi) je n'arrive à rien.

[Ericovitchi]

Ne vois tu pas que quand on additionne les équations :
f(1) =
f(2) =
f(3) =
---------------------
f(n) =

Tous les termes se simplifient deux à deux (par exemple le de la repmière ligne avec le de la seconde, et que c'est vrai pour toutes les lignes.
Il ne reste que le de la dernière ligne et le -1 de la première

Tu trouves quoi pour P et S ?

[anto17]

Merci beaucoup !!
Pour S, avec la formule donc S
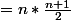
Donc

:we:

[Ericovitchi]

Bravo c'est ça, et bonne continuation