Valeurs d'adhérences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 29 Jan 2009, 08:49
par leon1789 » 29 Jan 2009, 08:49
leon1789 a écrit:P n'est pas majoré car pour tout
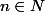
, le plus petit diviseur >1 de n!+1 est un nombre premier >n
D'ailleurs, si n+1 est un premier p, cette construction produit p (Théorème de Wilson !)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 29 Jan 2009, 11:23
par yos » 29 Jan 2009, 11:23
Nightmare a écrit:Non ce sont bien les ouverts ! Cependant, ce sont aussi des fermés !
Mais quand tu réunis {3n+1} et {3n+2}, tu n'as pas une suite arithmétique.
Ce n'est qu'une base d'ouverts que tu donnes?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Jan 2009, 11:32
par Nightmare » 29 Jan 2009, 11:32
Oui Yos tu as raison, ce n'est pas la définition des ouverts mais des voisinages ouverts.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Jan 2009, 17:26
par ThSQ » 29 Jan 2009, 17:26
Nightmare a écrit:Pfff, quelle preuve compliquée !
Pourquoi ne pas simplement écrire que :
On munie
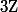
de la topologie où les ouverts sont les

où
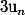
est une suite arithmétique quelconque.
Alors

L'ensemble de gauche n'est pas fermé, si l'ensemble des nombres premiers était fini, celui de droite le serait ! Contradiction
:lol3:
PS : Il est évident que la première phrase et le caractère extrêmement prétentieux qu'elle confère à ce poste n'est qu'une joke !
Jolie, c'est une des preuves du Grand Livre !
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 29 Jan 2009, 18:29
par Joker62 » 29 Jan 2009, 18:29
Le Grand Livre ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Jan 2009, 18:33
par ThSQ » 29 Jan 2009, 18:33

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 29 Jan 2009, 18:59
par leon1789 » 29 Jan 2009, 18:59
hé l'eau ,
j'ai une question ! :id:
Comme je ne crois pas au hasard dans l'élaboration des preuves mathématiques, il y a bien une explication au fait que cette preuve par l'absurde de P infini soit toujours citée. (c'est même la première dans le "grand livre")
Quand on écrit un truc, j'imagine que soit on y a réfléchi, soit c'est instinctif.
Vous écrivez (regardez-moi bien dans les yeux) cette preuve par l'absurde, ok. Est-ce par instinct ou par choix délibéré (si tel est le cas, quelle en est la raison ?) ?
Merci pour vos éventuelles réponses
(ha ben oui, faut être poli :zen: )
-
SimonB
 par SimonB » 29 Jan 2009, 19:05
par SimonB » 29 Jan 2009, 19:05
Ben, c'est d'une part par habitude (après avoir vu de nombreux profs faire comme ça), d'autre part par instinct (on a envie pour prouver une existence de remplacer le "il existe" par un "pour tout", donc on absurdise le tout). Mon prof de spé disait souvent : "quand je veux démontrer qu'il existe quelque chose, je suppose que ça n'existe pas et ôlala ça va pas". Ca m'a sûrement marqué...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Jan 2009, 19:13
par ThSQ » 29 Jan 2009, 19:13
leon1789 a écrit:Merci pour vos éventuelles réponses
Euclide c'est pas n'importe qui non plus. Son aura (ses Éléments sont souvent considérés comme le début des maths "axiomatiques") doit y être pour quelque-chose.
PS Et mon anneau de Krull ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 29 Jan 2009, 19:28
par leon1789 » 29 Jan 2009, 19:28
Merci pour vos réponses (mais j'en attends d'autres, pour avoir un bon éventail)
ThSQ a écrit:PS Et mon anneau de Krull ?
mé heuuu... je suis en GREVE aujourd'hui ! :pirate:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 29 Jan 2009, 19:35
par ffpower » 29 Jan 2009, 19:35
Pour moi,les preuves par l absurdes,je les fait par reflexe,mais c est un reflexe délibéré.C est que quand on veut prouver un truc,l absurde permet d obtenir des hypotheses supplémentaires(a savoir que la conclusion est fausse),ce qui peut forcément s avérer utile...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
, le plus petit diviseur >1 de n!+1 est un nombre premier >n
de la topologie où les ouverts sont les
où
est une suite arithmétique quelconque.