Les continus

[Facteur]

Une partie K de (X,d) est un continu si elle est compacte connexe et non vide.
Soit (Kn) une suite décroissante de de continus, on veut montrer que leur intersection K est un continu.
a) Montrer que K est un compact non vide.
b) Soit F un fermé qui ne rencontre pas K, montrer qu'il n tel que F ne rencontre pas Kn
c) Soient F et G deux fermés disjoints de X, montrer qu'il existe deux ouverts disjoints U, V tels que FcU et GcV
d) Montrer que K est un continu

Voilà j'ai réussi à montrer que K est un compact comme intersection de compact j'ai montré que K etait différent du vide.
Pour la b) j'ai écrit la contraposé je ne sais pas si c'est suffisant.
Pour la c) j'applique le lemme d'Urysohn
(avec une fonction f: x->d(x,F)/(d(x,F)+d(x,G)).
Donc j'ai montré que K est un compact non vide. Pour montrer que K est un continu il me reste à montrer que K est connexe mais je ne vois pas comment faire.

Merci de votre aide :happy2:

[ThSQ]

En prenant la topologie induite au besoin on peut se ramener à X compact (*).

Si K est l'union de deux fermes A et B, tu prends les ouverts U et V de c)

Soit C = X - U - V

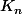rencontre C sinon cela contredit la connexité de 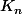(faire un dessin !).

Et le pb c'est que est donc une suite décroissante de compacts (*) non vides dont l'intersection est ....

[Nightmare]

Salut :happy3:

Ben, faudrait peut être utiliser le c) non? :lol3:

[Nightmare]

Oups en retard, désolé.

[ThSQ]

Et si on remplace connexe par connexe par arcs ? :doh: :biere:

[Facteur]

En prenant la topologie induite au besoin on peut se ramener à X compact (*).

Si K est l'union de deux fermes A et B, tu prends les ouverts U et V de c)

Soit C = X - U - V

rencontre C sinon cela contredit la connexité de (faire un dessin !).

Et le pb c'est que est donc une suite décroissante de compacts (*) non vides dont l'intersection est ....

Je ne comprends pas ton raisonnement. :triste:

[Facteur]

Bonjour, si j'ai bien compris on suppose K non connexe (K inclus dans deux ouverts non vides)
On prend le complementaire C qui est fermé (complémentaire d'une union d'ouvert). L'intersection avec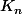 est non vide. (Je ne vois pas trop pourquoi car C et un fermé qui ne rencontre pas K(car K est inclus dans le complémentaire de C dans X) donc d'après b) il existe n tel que C ne rencontre pas 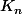??) :hein:
Je l'admet on a que est compact car intersection de fermé donc fermé dans X qui est compact. est décroissante donc est décroissante. C'est non vide par l'hypothèse que je n'ai pas compris. Donc on a une intersection décroissante de compacts non vides, donc l'intersection est non vide.
On a donc non vide ce qui est contradictoire.
Donc K connexe. C'est bien ça ?