Nombres complexes

[Huppasacee]

ton z² semble correct

as tu vérifié géométriquement ?

et si l'angle entre Ox ( axe des abscisses) et OM vaut theta ( tu le mesures avec le rapporteur )
tu places le point trouvé pour z² , disons N

l'angle de Ox avec ON vaudra 2 theta

Pour le module , je t'en ai déjà parlé

Vérifie

[tigre]

pour le module soit z=a+ib
module



ainsi vous trouverais
donc module de

[mamanmel]

J'ai mesuré 16. Est-ce que ça veut dire que le module de z vaut 4?

(J'ai beau chercher le backslash sur mon clavier, je ne le trouve pas.)

[tigre]

il fout faire l'argument aven c'est mieux (mais le 4 et juste)

[mamanmel]

Maintenant comment trouver les entiers n tels que soit un imaginaire?

[mamanmel]

Je ne comprends pas ce qu'ils entendent par "imaginaire".

[Huppasacee]

Re bonjour

Alors, as tu calculé l'argument de z²?
tu as :
8(racine de 3 + i)

alors cherchons l'argument

( au fait, il faut que tu apprennes à utiliser le cercle trigonométrique )


première remarque : la partie réelle est

et sa partie imaginaire est 8

donc , si nous plaçons l'image de z² dans le plan complexe, il sera dans le premier quadrant

( x > 0 et y > 0)

donc l'argument sera compris entre 0 et

maintenant , calculons tan (Arg z²)
c'est

donc

soit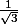

tu connais la tangente de l'argument de z², tu sais qu'il entre 0 et pi/2

donc tu connais l'argument de z²

Que trouves tu ?

donc tu connaîtra l'argument de z ( c'est la moitié de ce que tu auras trouvé )

tu sauras alors quel est l'argument de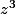 ( c'est Arg (z) * 3, de 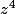( donc Arg(z)*4

et pour n quelconque

Arg (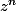 ) = n Arg(z)

pour qu'un nombre soit imaginaire, il faut qu'il n'ait pas de partie réelle, ou , traduit en terme d'argument :

Arg(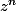) = , k appartenant à n

[mamanmel]

Bonsoir,
merci de m'être tjs fidel. Alors pour je trouve et donc

Juste?

[Huppasacee]

Là, tu n'as pas mis la moitié, tu as mis le double, tu ne crois pas ?

[mamanmel]

Oups...Effectivement. Donc ?

[Huppasacee]

pour le clavier qwerty :
http://upload.wikimedia.org/wikipedia/commons/thumb/6/62/KB_*Canadian_French.svg/800px-KB_Canadian_French.svg.png

le backslash semble être à gauche de la touche 1, tout en haut à gauche ( du moins pour le clavier canadien )

[Huppasacee]

Oups...Effectivement. Donc ?

oui , c'est cela

et maintenant , en multipliant cet angle par n , il faut que tu tombes ( dans le plan ) sur l'axe des coordonnées

c'est à dire que tu aies une valeur:
première valeur de n
ou encore une !

etc.