Pourriez-vous me rappeler comment trouver les racines de la fonction
Trigonométrie
8 messages
- Page 1 sur 1
Trigonométrie
par entropik » 05 Oct 2008, 22:32
Bonsoir,
Pourriez-vous me rappeler comment trouver les racines de la fonction)
? Je ne parviens pas à m'en souvenir
Pourriez-vous me rappeler comment trouver les racines de la fonction
par fatal_error » 05 Oct 2008, 23:19
salut,
=cos(x)/sin(x))
Mise au même dénominateur, on regarde le numérateur :
-cos(2x))
on developpe cos(2x) en fonction de sin(x)
-(1-sin^2(x)-sin^2(x))=2sin^2(x)+sin(x)-1)
On pose)
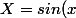et on résout
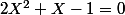
pis apres faut vérifier que les solutions annulent pas le dénominateur
Mise au même dénominateur, on regarde le numérateur :
on developpe cos(2x) en fonction de sin(x)
On pose
et on résout
pis apres faut vérifier que les solutions annulent pas le dénominateur
la vie est une fête 
par fatal_error » 05 Oct 2008, 23:29
Salut,
on peut mettre au même dénominateur:
-cos(2x)}{sin(2x)})
On utilise une formule trigo-cos(q)=2sin(\frac{p+q}{2})sin(\frac{p-q}{2})))
avec=cos(\frac{\pi}{2}-2x))
On obtiens alors
-cos(2x)}{sin(2x)}=\frac{2sin(\frac{\pi}{4})sin( \frac{\pi}{4}-2x)}{sin(2x)}=\frac{\sqrt{2}sin(\frac{\pi}{4}-2x)}{sin(2x)})
reste a resoudre
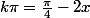
et vérifier les solutions par rapport au dénominateur
on peut mettre au même dénominateur:
On utilise une formule trigo
avec
On obtiens alors
reste a resoudre
et vérifier les solutions par rapport au dénominateur
la vie est une fête
par Benjamin » 06 Oct 2008, 09:55
fatal_error a écrit:On utilise une formule trigo
Il y a une petite erreur de signe, la formule, c'est
par phryte » 06 Oct 2008, 11:47
Slt.
1-cotg(2x) = 0 ==> cotg(2x)=1 (idem tg(2x)=1)
donc 2x = pi/4 + 2kpi
x=pi/2 + k.pi
1-cotg(2x) = 0 ==> cotg(2x)=1 (idem tg(2x)=1)
donc 2x = pi/4 + 2kpi
x=pi/2 + k.pi
par rene38 » 06 Oct 2008, 13:56
Bonjour
Bonne idée, mauvaise réalisation :phryte a écrit:Slt.1-cotg(2x) = 0 ==> cotg(2x)=1 (idem tg(2x)=1)
donc 2x = pi/4 + 2kpi
x=pi/2 + k.pi
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :