Saut,
leon1789 a écrit:oui, c'est vrai que les ... participent à la réalisation de l'erreur en quelque sorte.
Mais je voulais garder le style d'écrire de l'histoire initiale, pensant maintenir ainsi un suspense.
Tiens, ou est donc passé la rigueur que tu prônes pour les autres? Est-ce que tu utilises des pointillés pour tes démonstrations dans les séries? (c'est une question sincère)
Et tes réflexions sur le niveau des autres, c'est tout ce que tu arrives à dire quand tu es à court d'arguments? tu as bien expliqué ta position, crois-tu que rabaisser les autres va servir les idées que tu défends? Ah pardon, tu t'es excusé auprès d'une personne, quelle élégance! Perso je m'en fout, je suis apparemment très loin de ce que tu appelles un mathématicien (si j'ai bien compris c'est Bac+5 en maths (avec mention) et plus de 4000 messages sur le forum), mais tu pourrais rester correct avec ceux avec qui tu discutes.
leon1789 a écrit:Sinon, oui, il faut clairement utiliser ici le formalisme

:
soit
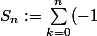^k E(k/2+1))
Alors

et

, ce qui permet non pas te justifier (c'était là l'histoire)

comme si la série

avait une limite (une valeur dans

), mais de conclure que S n'a pas de limite.
Mais avec ça, le charme de l'énoncé initial tombe à l'eau je trouve.
Oui, donc là je vais te faire une demi-fleur : je suis d'accord avec toi : si on veut formaliser la notation avec les pointillés on arrive à cette relation et à cette impossibilité de calculer la limite.
Maintenant on pourrais parler longtemps sur la "bonne" méthode à appliquer, mais pour moi si on supprime cette histoire d'écriture de somme infinie, la plupart des messages précédents sont justes si on accepte de ne pas trop tenir compte de la rigueur, tout comme ta démo (en même temps, cette énigme est supposé être un jeu, ça ne sert pas à grand chose de se prendre la tête comme cela...).
