Transvection ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
par MacManus » 04 Mai 2008, 16:14
Bonjour à tous!
Une transformation affine g :
est définie par :
 \in R^2, g(x,y) = (x',y'))
où :
x' = 2x+y-2 et y' = -x+2
La partie linéaire de g est la matrice A =
A n'est pas orthogonale donc g n'est pas une isométrie.
le polynôme caractéristique de A est :
^2)
donc A n'est pas diagonalisable. Ma question est donc :
Comment écrire g dans une base qui trigonalise A ??merci beaucoup.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 04 Mai 2008, 16:32
Tu peux l'écrire
dans une certaine base
(
pas sûr de comprendre la question )
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
par MacManus » 04 Mai 2008, 16:51
J'obtiens que
 = Vect[(1,-1)])
et
)
= 1
mais je ne répond pas à la question ! :hum:
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
par MacManus » 04 Mai 2008, 18:27
En fait j'ai oublié comment rendre une matrice non diagonalisable, en une matrice trigonalisable.
Bon... pour une matrice 2x2 le calcul n'est surement pas très difficile, mais j'ai tout de même une question :
Si ma matrice de départ est A =
n'est pas diagonalisable mais qu'elle possède 1 pour valeur propre double, je peux la trigonaliser sous la forme :
T =
Je sais que
 = Vect[u_1])
où
)
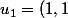j'ai le système suivant :
= u_1)
= au_1+u_2)
Comment trouver le vecteur
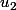
et
pour que
)
forme une base de T ??
Merci pour votre aide !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
