Bonjour,
je cherche à prouver que l'ensemble des matrices orthogonales carrées de taille 2 s'écrit sous la forme
cost sint
-sint cost
cost sint
sint -cost
Merci de votre aide.
Je me doute qu'il faut utiliser le déterminant mais je sais pas trop comment .
Matrices orthogonales carrées de taille 2
5 messages
- Page 1 sur 1
par seriousme » 15 Jan 2008, 22:04
En effet puisque les transposés des matrices :
, 
sont aussi orthogonales d'ordre 2 .
sont aussi orthogonales d'ordre 2 .
par seriousme » 15 Jan 2008, 22:42
Le produit donne :
Donc une interprétation possible est :
est un point du cercle trigonométrique,
Donc)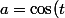
et )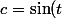
, ou le contraire mais cela revient au même .
est également un point du cercle trigonométrique .
Donc Donc)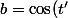
et )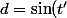
De plus
, donc le produit scalaire des vecteurs (a,c) et (b,d) est nul .
Donc il y a un angle de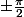
entre les vecteurs .
Donc
.
Si
:
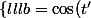 = \cos(t + \frac{\pi}{2}) & = & -\sin(t) \\<br />d = \sin(t') = \sin(t + \frac{\pi}{2}) & = & \cos(t) \\<br />\end{array*}<br />\right.)
Et si
:
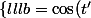 = \cos(t - \frac{\pi}{2}) & = & \sin(t) \\<br />d = \sin(t') = \sin(t - \frac{\pi}{2}) & = & -\cos(t) \\<br />\end{array*}<br />\right.)
Ce qui donne le résultat .
Donc une interprétation possible est :
Donc
Donc Donc
De plus
Donc il y a un angle de
Donc
Si
Et si
Ce qui donne le résultat .
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :