Intégration par partie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 17:18
par ptitmatteo » 09 Jan 2008, 17:18
oui mais il faut aussi changé la variable
il me samble?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 17:32
par ptitmatteo » 09 Jan 2008, 17:32
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Jan 2008, 17:43
par Monsieur23 » 09 Jan 2008, 17:43
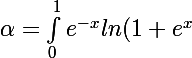.dx = \int_1^e \frac1t Ln(1+t) \frac1t .dt)
Exp(-x) = 1 / Exp(x) se transforme en 1/t
Ln(1+Exp(x) ) se transforme en Ln(1+t)
dx devient dt/t
« Je ne suis pas un numéro, je suis un homme libre ! »
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 18:19
par ptitmatteo » 09 Jan 2008, 18:19
b°
calculer alors J en utilisant une intégration par parties et le résultat de I=
})
on pose
u'(x)=
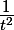
et v(x)=ln(1+t)
u(x)=
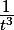
et v'(x)=
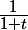
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 18:38
par ptitmatteo » 09 Jan 2008, 18:38
b°
calculer alors J en utilisant une intégration par parties et le résultat de I=
})
on pose
u'(x)=
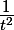
et v(x)=ln(1+t)
u(x)=
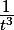
et v'(x)=
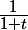
J=
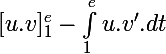
J=
]_1^e-\int_1^e\frac{-2}{t^3.(1+t)}.dt)
J=
+2.ln(2)+\int_1^e\frac{-2}{t^3.(1+t)}.dt)
mais le probleme c'est je ne sais pas si je doit ré-intégré ou pas
}.dt)
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Jan 2008, 19:37
par Monsieur23 » 09 Jan 2008, 19:37
Tu t'es simplement gourré dans ta fonction u.
Si u'(t) = 1/t², ca fait u(x) = -1/t ( et pas -2/t^3 )
Comme ça tu retombes sur l'intégrale de la question précédente
« Je ne suis pas un numéro, je suis un homme libre ! »
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 19:56
par ptitmatteo » 09 Jan 2008, 19:56
ah oui
I=
})
on pose
u'(x)=
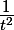
et v(x)=ln(1+t)
u(x)=
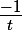
et v'(x)=
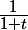
J=
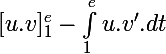
J=
]_1^e-\int_1^e\frac{-1}{t.(1+t)}.dt)
J=
+ln(2)+\int_1^e\frac{-1}{t.(1+t)}.dt)
comme dit dans la question b
}.dt)
=
)
donc
J=
+ln(2)+1+ln(\frac{2}{e+1}))
es que c'est juste
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 20:41
par ptitmatteo » 09 Jan 2008, 20:41
es que j'ai juste
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Jan 2008, 21:06
par Monsieur23 » 09 Jan 2008, 21:06
Je pense trouver ça aussi.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 09 Jan 2008, 21:17
par ptitmatteo » 09 Jan 2008, 21:17
merci
1° claculer la dériver de la fonction définie sur ]
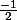
;

[ par f(x)=
^{\frac{3}{2}})
on pose f=u o g
u(x)=
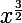
et g(x)=2x+1
u'(x)=
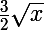
et g'(x)=2
alors f '=u' o g . g'
donc
f'(x)=
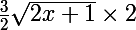
f'(x)=
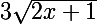
es que c'est juste
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 10 Jan 2008, 17:58
par Monsieur23 » 10 Jan 2008, 17:58
C'est ça .
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 10 Jan 2008, 18:05
par Babe » 10 Jan 2008, 18:05
la dérivée de
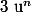
est
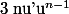
^{3/2})=(3/2)2(2x+1)^{1/2}=3(2x+1)^{1/2})
c'est bien ca
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 13 Jan 2008, 15:35
par ptitmatteo » 13 Jan 2008, 15:35
Monsieur23 a écrit:} = \frac{A}{t} + \frac{B}{t+1})
On multiplie tout par t :
} = A + \frac{tB}{t+1})
On prend t=0 :
A = 1
On revient au départ, on multiplie tout par t+1 :
A}{t} + B)
On prend t=-1 :
-1 = B
Mais c'est sûr qu'en prenant A=0 et B=1/t, ça marche ( mais c'est inutile ).
En fait, avec ta méthode, il ne faut pas résoudre le système comme tu l'as fait.
Tu as (A+B)t + A = 1
En identifiant les coefficients, Ca te fait A+B = 0 ( coeff en t ) et A = 1 ( coeff constant ).
C'est plus clair ?
je pence que ne peut pas passer par cette technique car dans l'énnoncé il est écris qu'il faut déterminer les réels A et B tels que pour tout réel t strictement positif alors on peut pas prendre
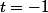
???
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 13 Jan 2008, 15:38
par Monsieur23 » 13 Jan 2008, 15:38
Oui, je m'en suis rendu compte après.
Mais bon, si c'est vrai pour tout t, c'est à fortiori vrai pour les t > 0.
Sinon tu utilises l'autre méthode :
Tu as (A+B)t + A = 1
En identifiant les coefficients, Ca te fait A+B = 0 ( coeff en t ) et A = 1 ( coeff constant ).
« Je ne suis pas un numéro, je suis un homme libre ! »
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 13 Jan 2008, 15:53
par ptitmatteo » 13 Jan 2008, 15:53
ok mais es que je prend
} = \frac{A}{t} + \frac{B}{t+1})
On multiplie tout par t :
} = A + \frac{tB}{t+1})
On prend t=0 :
A = 1
et aprés on pourrais en déduire A+B = 0 avec A = 1
?????
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 13 Jan 2008, 16:13
par ptitmatteo » 13 Jan 2008, 16:13
je pas tout compris
(A+B)t + A = 1
En identifiant les coefficients,
Ca te fait A+B = 0 ( coeff en t ) et A = 1 ( coeff constant ).
mais la je ne comprend pas pourquoi on dit que A+B=0
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 13 Jan 2008, 16:23
par ptitmatteo » 13 Jan 2008, 16:23
ah j'ai peut compri
} = \frac{A}{t} + \frac{B}{t+1})
On multiplie tout par t :
} = A + \frac{tB}{t+1})
On prend t=0 :
A = 1
et comme j'ai montré que
1=(A+B).t+A
on remplace A=1
1=(1+B).t+1
(1+B).t=0 si l'un des deux est égale a 0
donc
1+B=0
B=-1
es que c'est ça??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
