Nature d'une série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 21 Oct 2007, 10:09
par exilim » 21 Oct 2007, 10:09
bonjour!
Je n'arrive pas à déterminer la nature de la série de terme général
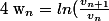)
où
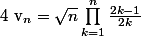
En bidouillant un peu,j'arrive à
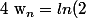+\frac{1}{2} ln (\frac{n}{n+1})+ln(2n+1))
mais ça ne m'aide pas vraiment... Je pense qu'il me suffirait d'avoir uniquement des séries convergentes, ou une seule série divergente pour pouvoir conclure, mais la ce n'est pas le cas!
Merci de votre aide!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Oct 2007, 10:33
par Joker62 » 21 Oct 2007, 10:33
ln(n/(n+1)) = ln(1 - 1/n) ~ -1/n
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 21 Oct 2007, 10:36
par klevia » 21 Oct 2007, 10:36
En supposant que ton Wn soit juste ( ce dont je doute, sans te vexer), on voit immédiatement que le terme général de la série ne tend pas vers 0 quand n tends vers l'infin donc la série diverge...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Oct 2007, 10:39
par Joker62 » 21 Oct 2007, 10:39
Bonne remarque sur la justesse du résultat, et encore meilleure remarque sur la limite du terme général :D
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 21 Oct 2007, 11:03
par exilim » 21 Oct 2007, 11:03
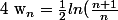+ln(\frac{2n+1}{2n+2}))
vous parait-il plus correct ?
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 21 Oct 2007, 11:28
par klevia » 21 Oct 2007, 11:28
Ok j'ai pareil ..
maintenant n+1/n = 1+ 1/n tu peux faire un petit DL
(2n+1)/(2n+2) = 1 - 1/(2n+2) tu peux aussi faire un DL.
Puis tu regroupes et tu vois ce que cela donne... Je l'ai pas fait mais ça devrait marcher ...
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 21 Oct 2007, 11:40
par alben » 21 Oct 2007, 11:40
Pourquoi tu n'utilises pas ce que tu as fait hier
^2=1+\frac 1{4n(n+1)})
d'où
}))
et pour t>0 ln(1+t)<t
ce qui te donne
}=\frac 18[\frac 1n -\frac 1{n+1}])
La deuxième série est telescopique et wn est donc bien convergente
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 21 Oct 2007, 11:46
par klevia » 21 Oct 2007, 11:46
ah, il y avait des questions avant qui aidaient ...
Désolé je ne savais pas
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 21 Oct 2007, 12:12
par exilim » 21 Oct 2007, 12:12
la question précédente montrait just que (vn) était croissante. Alben, je ne suis pas arrivé aux résultats que vous m'avez donné hier mais j'ai tout de même réussi a m'en sortir. (merci klevia je crois que je vais tenter les DL)
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Oct 2007, 12:44
par rifly01 » 21 Oct 2007, 12:44
Bonjour,
Moi j'aurai fait :
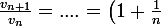^{1/2}\left(1+\frac{3}{2n}\right)\left(1+\frac{1}{n} \right)^{-1}=\left(1+\frac{3}{2n}\right)\left(1+\frac{1}{n} \right)^{-1/2}=1+\frac{1}{n}+O\left(\frac{1}{n^2}\right))
Et
=\frac{1}{n}+O \left(\frac{1}{n^2}\right))
Une fois ici, j'aurai gentillement conclu,qu'elle est divergente.

Je ne sais pas si c'est juste mais c'est ce que j'aurai certainement fait.
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 21 Oct 2007, 12:47
par exilim » 21 Oct 2007, 12:47
euh... la je suis perdu! la série de terme général wn est-elle convergente ou divergente? (peut-etre un petit indice: dans la question suivante il faut en déduire que la suite (vn) est convergente)
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 21 Oct 2007, 15:00
par alben » 21 Oct 2007, 15:00
Je suis désolé mais c'est quand même très tres tres simple
}{sqrt n(2n+2)}\sqrt{n}\prod_{k=1}^{n} \frac{2k-1}{2k}=\frac{sqrt{n+1}(2n+1)}{2sqrt n(n+1)}v_n)
On a donc
^2=\frac{(n+1)(2n+1)^2}{4n(n+1)^2})
Après simplification par n+1 et développement de la fraction
^2=\frac{4n^2+4n+1}{4n^2+4n}=1+\frac 1{4n(n+1)})
Jusqu'ici, un mauvais élève de seconde ne devrait avoir aucun problème à suivre :hum:
Ensuite, voir mon message précédent. Cette série est nécessairement convergente et sa somme est légèrement inférieure à 1/8 !
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 21 Oct 2007, 15:16
par klevia » 21 Oct 2007, 15:16
vraiment bien vu, alben ... Faut que j'apprenne à être plus "percutante" dans mes demos... Trouver directement le bon argument et non pas passer par des méthodes bourrines ...
Encore bravo !!
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Oct 2007, 16:34
par rifly01 » 21 Oct 2007, 16:34
Re -
Je l'ai refait avec Maple. Il trouve que c'est une série convergente et me donne aussi sa somme. Elle vaut 1.
[CENTER]

[/CENTER]
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 21 Oct 2007, 17:07
par alben » 21 Oct 2007, 17:07
erreur de signe à la première ligne, dans le numérateur à l'intérieur du produit c'est 2k-1 et non 2k+1.
Mais Bravo à toi et mapple ! Pourquoi faire simple quand on peut compliquer ?
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 21 Oct 2007, 21:39
par exilim » 21 Oct 2007, 21:39
merci a tous! (et surement à bientot ;) )
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Oct 2007, 23:06
par rifly01 » 21 Oct 2007, 23:06
Merci pour le complément,
J'ai trouvé la valeur exacte de la somme, en corrigeant l'erreur, elle vaut :
}{2})
Et je viens de me rendre compte que j'ai fait la même erreur dans ma première intervention. Autrement dit, j'ai bien raison,
 \quad \mbox{ avec } v_n = \sqrt{n}\prod_{k=1}^{n}\frac{2k+1}{2k})
diverge.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Oct 2007, 17:25
par Joker62 » 22 Oct 2007, 17:25
Pour Klevia, faut savoir qu'alben n'a pas trouver ça en rédigeant directement, il a user bien du papier avant :D
Enfin j'parle pour alben, mais bon j'suppose que c'est ça :)
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 22 Oct 2007, 18:44
par alben » 22 Oct 2007, 18:44
Joker62 a écrit:Pour Klevia, faut savoir qu'alben n'a pas trouver ça en rédigeant directement, il a user bien du papier avant

Enfin j'parle pour alben, mais bon j'suppose que c'est ça

Tout à fait, Joker, comme klevia, j'ai commencé par des méthodes bourrines...
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 22 Oct 2007, 20:23
par exilim » 22 Oct 2007, 20:23
Je suis enfin parvenu à obtenir la convergence de wn (merci a tous!), mais je voudrai une confirmation que mon raisonnement qui en découle est juste:
la série de terme général wn converge, donc wn --> 0 donc (vn+1/vn) --> 1 donc la suite (vn) converge (la je pense qu'il manque une petite justification mais je ne sais pas trop laquelle)...
Comment je peux en déduire une comparaison de un et de

pour tout n>0 (L est la limite de vn) j'aurais tendance a dire que
un<

(justification par la croissance de vn?)
Merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités