Bon alors je pense avoir trouvé une solution qui marche pour tous les cas en utilisant le raisonement de fahr451
Alors je récapitule : Soit E un espace vectoriel de dimension finie n sur un corp

commutatif.
J'ai

des sous espaces vectoriels de E .
Je veux démontrer que

ont même dimension alors ils ont un supplémentaire en commun mais ça me marche pas toujours ! Mais si le corps est infini alors ça marche pour tout

quelconque (Notons que le cas p=2 marche pour n'importe quel corps ).
Alors le but est d'utiliser le raisonement de fahr en disant qu'il existera au moins un vecteur
)
et faire la récurrence après .
Alors pour notre implication qui nous intéresse( la moins triviale) est de montrer que si

ont même dimension alors ils ont même supplémentaire deux cas se présentent :
Si

, alors le seul supplémentaire commun est réduit à 0 car : soit G un supplémentaire commun , alors

donc
)
et
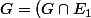 \cup ... \cup (G\cap E_p) =0)
et dans ce cas tous les
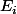
vallent E tout entier . Et 0 l'unique supplémentaire.
Sinon il existe un élément (non nul)
)
et on termine par récurrence ...
Remarque : Si on travaille avec un corps fini , on a des ennuis parce que on sait que E a un nombre fini de vecteurs et on peut écrire E comme la réunion disjointes de ses vecteurs et le résultat est faux car chaque espace engendré par un vecteur n'est pas E tout entier .
