Bonsoir,
je recherche un moyen d'obtenir une fonction mathématique approchante,
en fonction de valeurs contenues dans une matrice.
J'ai une partie des données correspondant à un temps de déplacement en fonction de position en 'X' et en 'Y' sous forme matriciel, j'aimerais obtenir une équation, afin d'avoir des valeurs suivant des coordonnées que je rentrerai.
Modèle mathématique
7 messages
- Page 1 sur 1
Non inscrit a écrit:Bonsoir,
je recherche un moyen d'obtenir une fonction mathématique approchante,
en fonction de valeurs contenues dans une matrice.
J'ai une partie des données correspondant à un temps de déplacement en fonction de position en 'X' et en 'Y' sous forme matriciel, j'aimerais obtenir une équation, afin d'avoir des valeurs suivant des coordonnées que je rentrerai.
Je ne vois pas ce que tu veux ! Pose ton problème ! Peut-être que quelqu'un y répondra...Mais tant que tu ne dis pas plus précisément ce que tu cherches, je pense que personne ne pourra t'y aider, en tous cas, moi je ne comprends rien. Désolé !
Salut !
Peut-être pour les splines cubiques définies par morceaux.
Si ça t'intéresse, tu peux construire ta courbe "approchante" au fur et à mesure d'ajouter les points en résolvant à chaque étape un petit système.
Bon, il nous faut des points, disons .
.
Pour une telle spline, on peut définir paramétriquement les points par,Y(t))) (en reprenant tes notations) où
(en reprenant tes notations) où  est un entier qui se ballade entre
est un entier qui se ballade entre  et
et  .
.
Je vais alors poser) , et appeler
, et appeler ) et
et ) mes points de contrôle avant et après mes points
mes points de contrôle avant et après mes points 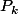 . (B comme Before et A comme After, parce qu'en français, ça merdouille un peu : Avant Après ... enfin bref).
. (B comme Before et A comme After, parce qu'en français, ça merdouille un peu : Avant Après ... enfin bref).
Les définitions paramétriques sont :
[INDENT]=(1-t)^3x_k+3t(1-t)^2x_k^a+3t^2(1-t)x_{k+1}^b+t^3x_{k+1})
=(1-t)^3y_k+3t(1-t)^2y_k^a+3t^2(1-t)y_{k+1}^b+t^3y_{k+1})
[/INDENT]pour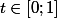 .
.
Avec ce genre de courbe définie par morceaux, tu peux avoir un assez bon contrôle sur les courbures. En particulier, tu peux "régler" les demi-tangentes "avant" et "après" les points de contrôle, genre :
[CENTER] [/CENTER]
[/CENTER]
Mais si tu veux avoir une courbe un peu plus "lisse", tu dois faire en sorte que les (demi-)tangentes "précédentes" et "suivantes" aient la même direction, autrement dit que les vecteurs et
et  aient la même direction. Une méthode consiste à se débrouiller pour avoir le point
aient la même direction. Une méthode consiste à se débrouiller pour avoir le point 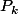 sur le segment
sur le segment  .
.
Tu peux aussi jeter un coup d'oeil sur Wiki : Ici
Peut-être pour les splines cubiques définies par morceaux.
Si ça t'intéresse, tu peux construire ta courbe "approchante" au fur et à mesure d'ajouter les points en résolvant à chaque étape un petit système.
Bon, il nous faut des points, disons
Pour une telle spline, on peut définir paramétriquement les points par
Je vais alors poser
Les définitions paramétriques sont :
[INDENT]
[/INDENT]pour
Avec ce genre de courbe définie par morceaux, tu peux avoir un assez bon contrôle sur les courbures. En particulier, tu peux "régler" les demi-tangentes "avant" et "après" les points de contrôle, genre :
[CENTER]
 [/CENTER]
[/CENTER]Mais si tu veux avoir une courbe un peu plus "lisse", tu dois faire en sorte que les (demi-)tangentes "précédentes" et "suivantes" aient la même direction, autrement dit que les vecteurs
Tu peux aussi jeter un coup d'oeil sur Wiki : Ici
Salut !
Personnellement, j'avais rencontré ce problème quand j'étais en 1re, lorsque j'ai voulu faire un petit programme dessin (sous TPascal); en Terminale, je l'avais refait en Delphi avec manipulation des points de contrôle et sans aucune condition sur les points de contrôle, ça marchait pas mal et ce qui permet d'avoir des points de rebroussement. Pour avoir du "bien lisse", on peut imposer d'avoir des points de contrôle "symétriques" par rapports aux points ( sauf pour le premier et le dernier).
Et dans le premier post, j'ai bien dit "peut-être". Attendons ce que "Non inscrit" va nous répondre (je suis peut-être complètement HS).
Personnellement, j'avais rencontré ce problème quand j'étais en 1re, lorsque j'ai voulu faire un petit programme dessin (sous TPascal); en Terminale, je l'avais refait en Delphi avec manipulation des points de contrôle et sans aucune condition sur les points de contrôle, ça marchait pas mal et ce qui permet d'avoir des points de rebroussement. Pour avoir du "bien lisse", on peut imposer d'avoir des points de contrôle "symétriques" par rapports aux points ( sauf pour le premier et le dernier).
Et dans le premier post, j'ai bien dit "peut-être". Attendons ce que "Non inscrit" va nous répondre (je suis peut-être complètement HS).
Ouille
Ok pour la leçon.
Mon exposé n;)était pas très claire, mais la solution plus simple que je ne pensais.
L;)éloignement par rapport au centre de mon repère était en arc de cercle.
10 9 9 8 8 7 7 7 7 7 8 8 9 9 10
9 8 8 7 7 6 6 6 6 6 7 7 8 8 9
9 8 7 6 6 5 5 5 5 5 6 6 7 8 9
8 7 6 6 5 4 4 4 4 4 5 6 6 7 8
8 7 6 5 4 4 3 3 3 4 4 5 6 7 8
7 6 5 4 4 3 3 3 3 3 4 4 5 6 7
7 6 5 4 3 3 3 3 3 3 3 4 5 6 7
7 6 5 4 3 3 3 0 3 3 3 4 5 6 7
7 6 5 4 3 3 3 3 3 3 3 4 5 6 7
7 6 5 4 4 3 3 3 3 3 4 4 5 6 7
8 7 6 5 4 4 3 3 3 4 4 5 6 7 8
8 7 6 6 5 4 4 4 4 4 5 6 6 7 8
9 8 7 6 6 5 5 5 5 5 6 6 7 8 9
9 8 8 7 7 6 6 6 6 6 7 7 8 8 9
10 9 9 8 8 7 7 7 7 7 8 8 9 9 10
Il ne m;)a fallu que trouver les valeurs sur un axe et utiliser Pythagore plus une recherche
dans un tableau de solution.
Certes, c;)est moins Mathématique mais c;)était plus à ma porter que les courbes de Béziers.
Merci à tous pour votre temps passé à me répondre.
Ok pour la leçon.
Mon exposé n;)était pas très claire, mais la solution plus simple que je ne pensais.
L;)éloignement par rapport au centre de mon repère était en arc de cercle.
10 9 9 8 8 7 7 7 7 7 8 8 9 9 10
9 8 8 7 7 6 6 6 6 6 7 7 8 8 9
9 8 7 6 6 5 5 5 5 5 6 6 7 8 9
8 7 6 6 5 4 4 4 4 4 5 6 6 7 8
8 7 6 5 4 4 3 3 3 4 4 5 6 7 8
7 6 5 4 4 3 3 3 3 3 4 4 5 6 7
7 6 5 4 3 3 3 3 3 3 3 4 5 6 7
7 6 5 4 3 3 3 0 3 3 3 4 5 6 7
7 6 5 4 3 3 3 3 3 3 3 4 5 6 7
7 6 5 4 4 3 3 3 3 3 4 4 5 6 7
8 7 6 5 4 4 3 3 3 4 4 5 6 7 8
8 7 6 6 5 4 4 4 4 4 5 6 6 7 8
9 8 7 6 6 5 5 5 5 5 6 6 7 8 9
9 8 8 7 7 6 6 6 6 6 7 7 8 8 9
10 9 9 8 8 7 7 7 7 7 8 8 9 9 10
Il ne m;)a fallu que trouver les valeurs sur un axe et utiliser Pythagore plus une recherche
dans un tableau de solution.
Certes, c;)est moins Mathématique mais c;)était plus à ma porter que les courbes de Béziers.
Merci à tous pour votre temps passé à me répondre.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
