Défi à tiroirs
46 messages
- Page 2 sur 3 - 1, 2, 3
Avec l'hypothèse que la suite converge vers 0, c'est mieux en effet:
Si k=1,
en posant , avec a et b premiers entre eux,
, avec a et b premiers entre eux,
la suite converge-t-elle modulo 1 si et seulement si:
converge-t-elle modulo 1 si et seulement si:
*x est dans ]0,1[ ou
*x est un entier tels que b divise une puissance de x.
Si k>1, on retrouve la complexité de mon message précédent:
exemple tend vers 0 modulo 1.
tend vers 0 modulo 1.
Cela a l'air difficile de trouver l'ensemble des conditions.
Je peux quand même dire qu'il suffit que les soient entre 0 et 1!
soient entre 0 et 1!
Je me sens perdu au fond du deuxième tiroir! :triste:
Je ne suis pas sûr que ce soit de mon niveau...
Si k=1,
en posant
la suite
*x est dans ]0,1[ ou
*x est un entier tels que b divise une puissance de x.
Si k>1, on retrouve la complexité de mon message précédent:
exemple
Cela a l'air difficile de trouver l'ensemble des conditions.
Je peux quand même dire qu'il suffit que les
Je me sens perdu au fond du deuxième tiroir! :triste:
Je ne suis pas sûr que ce soit de mon niveau...
En fait le cas 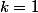 se traite comme le 1°) pratiquement au mot près , il suffit de l'écrire ( d'ailleurs r pourrait très bien être réel non nul ) . Les
se traite comme le 1°) pratiquement au mot près , il suffit de l'écrire ( d'ailleurs r pourrait très bien être réel non nul ) . Les  inférieurs à 1 disparaissent de la somme donc le seul cas à étudier est celui ou les
inférieurs à 1 disparaissent de la somme donc le seul cas à étudier est celui ou les  sont tous supérieurs à 1 . Pour
sont tous supérieurs à 1 . Pour 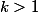 , la partie délicate ( je vous laisse chercher ) est de montrer que si
, la partie délicate ( je vous laisse chercher ) est de montrer que si 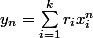 converge vers 0 modulo 1 alors il existe des rationnels non nuls
converge vers 0 modulo 1 alors il existe des rationnels non nuls  tels que
tels que  converge vers 0 modulo 1 et de faire jouer la récurrence .
converge vers 0 modulo 1 et de faire jouer la récurrence .
Imod
Imod
Pour k=1, on est d'accord, si la suite 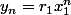 converge vers 0 modulo 1 alors soit
converge vers 0 modulo 1 alors soit  est dans ]0,1[, soit il est entier. [réciproque fausse]
est dans ]0,1[, soit il est entier. [réciproque fausse]
On raisonne par récurrence en supposant que si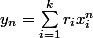 converge vers 0 modulo 1 pour un certain k, alors les
converge vers 0 modulo 1 pour un certain k, alors les  sont soit dans ]0,1[, soit entiers.
sont soit dans ]0,1[, soit entiers.
On va montrer que cela marche encore en remplaçant k par k+1.
On suppose donc que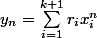 converge vers 0 modulo 1.
converge vers 0 modulo 1.
Si l'un des est dans ]0,1[, il disparait de la somme, et c'est fini.
est dans ]0,1[, il disparait de la somme, et c'est fini.
Sinon, notons) une suite telle que
une suite telle que 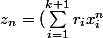-u_n}) converge vers 0 (tout court).
converge vers 0 (tout court).
En posant et
et 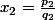 , et en définissant
, et en définissant 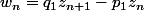 ,
,
on obtient
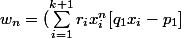-q_1u_{n+1}+p_1u_n})
Or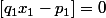 .
.
Il reste donc simplement:
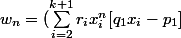-q_1u_{n+1}+p_1u_n})
Ce qui signifie que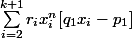 converge vers 0 modulo 1.
converge vers 0 modulo 1.
En posant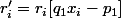 ,
,
cela donne
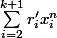 converge vers 0 modulo 1.
converge vers 0 modulo 1.
D'après l'hypothèse de récurrence, tous les pour i entre 2 et k+1 sont entiers.
pour i entre 2 et k+1 sont entiers.
En refaisant le même travail pour éliminer le , on déduit que tous les
, on déduit que tous les  pour i entre 1 et k sont entiers.
pour i entre 1 et k sont entiers.
Ainsi c'est gagné, tous les pour i entre 1 et k+1 sont entiers.
pour i entre 1 et k+1 sont entiers.
Et la propriété "deuxième tiroir" est démontrée par récurrence.
On raisonne par récurrence en supposant que si
On va montrer que cela marche encore en remplaçant k par k+1.
On suppose donc que
Si l'un des
Sinon, notons
En posant
on obtient
Or
Il reste donc simplement:
Ce qui signifie que
En posant
cela donne
D'après l'hypothèse de récurrence, tous les
En refaisant le même travail pour éliminer le
Ainsi c'est gagné, tous les
Et la propriété "deuxième tiroir" est démontrée par récurrence.
46 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
