K^{p-1}=1[p²]
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Mai 2007, 15:32
par aviateurpilot » 30 Mai 2007, 15:32
salut,
voila un exo facile mais intéressant.
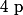
premier.
calculer
\}))
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Juin 2007, 12:27
par aviateurpilot » 01 Juin 2007, 12:27
dans ma solution j'ai posé:

\})
et j'ai montré:
i)
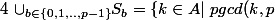=1\})
ii)
\in \{0,1,..,p-1\}^2,\ i\neq j\ \Longleftrightarrow \ S_i\cap S_j=\emptyset)
iii)
=card(S_b))
et j'ai conclu le
\})=card(S_0))
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 01 Juin 2007, 14:42
par redwolf » 01 Juin 2007, 14:42
*)
est cyclique si je me souviens bien. Les éléments d'ordre divisant

sont donc au nombre de

(l'ordre du groupe,
)
est bien divisible par

) .
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Juin 2007, 14:51
par aviateurpilot » 01 Juin 2007, 14:51
redwolf a écrit:*)
est cyclique si je me souviens bien. Les éléments d'ordre divisant

sont donc au nombre de

(l'ordre du groupe,
)
est bien divisible par

) .
ce que tu as utilisé derectement ici, c'est ce qu'on veux montrer.
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 01 Juin 2007, 20:21
par Lierre Aeripz » 01 Juin 2007, 20:21
aviateurpilot a écrit:dans ma solution j'ai posé:

\})
et j'ai montré:
i)

ii)
\in \{0,1,..,p-1\}^2,\ i\neq j\ \Longleftrightarrow \ S_i\cap S_j=\emptyset)
iii)
=card(S_b))
et j'ai conclu le
\})=card(S_0))
Que
\})=card(S_0))
est un truisme...
De plus, il me semble que le raisonnement est faux.
En mettant bout à bout tes trois points, on obtient

. Or

. Absurde car

...
Es-tu bien sûr du point (i) ? (Cas p = 2 ?)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 01 Juin 2007, 20:28
par fahr451 » 01 Juin 2007, 20:28
i est faux pour pour p >2
k^(p-1) = 1 (mod p) uniquement pour k et p premier entre eux
pour k = p,2p,3p,... on a k^(p-1) congru à 0 mod p^2
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Juin 2007, 22:38
par aviateurpilot » 01 Juin 2007, 22:38
Lierre Aeripz a écrit:Que
\})=card(S_0))
est un truisme...
De plus, il me semble que le raisonnement est faux.
En mettant bout à bout tes trois points, on obtient

. Or

. Absurde car

...
Es-tu bien sûr du point (i) ? (Cas p = 2 ?)
il est tres tres evident que
\})=card(S_0))
car
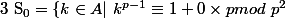\})
lol.
en plus en mettant bout à bout mes trois points, on obtient
 =card(\{k\in A|\ pgcd(p,k)=1\})=p^2-p)
.
donc
=p-1)
j'ai just oublié de retrancher les multiples de

dans

j'ai deja resolu cet exercice ici avant de le posté dans le forum
http://www.mathlinks.ro/viewtopic.php?t=151583pour le cas de

\})=2-1)
qui es vrai. car la seule solution c'est

-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 02 Juin 2007, 09:56
par Lierre Aeripz » 02 Juin 2007, 09:56
aviateurpilot a écrit:il est tres tres evident que
\})=card(S_0))
car
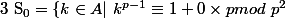\})
lol.
en plus en mettant bout à bout mes trois points, on obtient
 =card(\{k\in A|\ pgcd(p,k)=1\})=p^2-p)
.
donc
=p-1)
j'ai just oublié de retrancher les multiples de

dans

j'ai deja resolu cet exercice ici avant de le posté dans le forum
http://www.mathlinks.ro/viewtopic.php?t=151583pour le cas de

\})=2-1)
qui es vrai. car la seule solution c'est

Dialogue de sourd : nous sommes tout à fait d'accord.
\})=card(S_0))
est un truisme et ton premier message contenait des erreurs

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
est un truisme...
. Or
. Absurde car
...
car
lol.
.
dans
j'ai deja resolu cet exercice ici avant de le posté dans le forum http://www.mathlinks.ro/viewtopic.php?t=151583