Bonjour!
:briques: J'ai dû mal à justifier dans cet exercice sur les complexes. ET je ne suis pas très sûr de mes réponses. Pouvez-vous m'aider? :briques:
Enoncé:
Soit z un nombre complexe différent de -2i et z'=(z-2)/(z+2i).
On note le point M le point d'affixe z dans le plan complexe P de repère ortho normal direct (O;(vecteur)u; (vecteur)v) et M le point daffixe z.
Soit A le point d'affixe a=-2i et B le point d'affixe b=2.
Dire si les propositions suivantes sont vraies ou fausses et justifier votre réponse.
1) L'ensemble des points M de P tels que OM'=1 est l'ensemble {W}, où W est le point d'affixe 1-i.
2) L'ensemble des points M de P tels que M'appartient à l'axe des ordonnées est le cercle de diamètre [AB] privé du point A.
3) L'ensemble des points M de P tels que z' est un réel positif est la droite (AB) privé du point A.
4) L'ensemble des points M de P tels que arg ( z')=-pi/2 est l'ensemble E (Les points A et B sont exclus de E).
5) L'ensemble des points M de P tels que OM'=V2 (V représente la racine) est le cercle de centre le point C d'affixe -2-4i et de rayon 4.
Voici que j'ai fait:
1/ z different de -2i
OM'=z-2/z+2i
1=-2i+2i-2/-2i+2i+2i
1=-2/2i
1=-1/i
1*i=-1
i=-1
W=-1-i.
Donc FAUX
2/ je ne vois pas comment faire.
3/ je bloque.
4/ arg (z')=-pi/2 (2 pi)
z différent de -2i
s'écrit ((vecteurs) MA,MB)=-pi/2 (2pi)
M différent A; M différent B
L' ensemble cherché est l'un des demi-cercles de diamètre [AB] privé de A et de B.
Donc VRAI
5/ OM'=z-2/z+2i
V2=-2i+2i-2/-2i+2i+2i
V2=-2/2i
V2=-1/i
iV2=-1
C=-1/iV2
C=-V2/2i
Et je bloque.
Merci
Nombres complexes je coince
3 messages
- Page 1 sur 1
salut,
rappel : si z1 et z2 sont les affixes de M1 et M2 alors:

donc ici
OM'=1

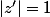


BM=AM
donc l'ensemble des poins M forme la mediatrice de [AB] donc....
 est un imaginaire pur
est un imaginaire pur
=\frac{\pi}{2}+k\pi)
...
1) L'ensemble des points M de P tels que OM'=1 est l'ensemble {W}, où W est le point d'affixe 1-i.
rappel : si z1 et z2 sont les affixes de M1 et M2 alors:
donc ici
OM'=1
BM=AM
donc l'ensemble des poins M forme la mediatrice de [AB] donc....
2) L'ensemble des points M de P tels que M'appartient à l'axe des ordonnées est le cercle de diamètre [AB] privé du point A.
...
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
