Rappports inférieurs à 10
23 messages
- Page 1 sur 2 - 1, 2
rappports inférieurs à 10
on a N1=a*1000 + b*100 + c*10 +d
N2=a*100+b*10+C
N3=A*100 + B*10 +C
N2<N3
N1>N3
je pense que N1/N3 <10
comment le démontrer ? (démontrer que c'est vrai ou démontrer que c'est faux)
une idée ?
N2=a*100+b*10+C
N3=A*100 + B*10 +C
N2<N3
N1>N3
je pense que N1/N3 <10
comment le démontrer ? (démontrer que c'est vrai ou démontrer que c'est faux)
une idée ?
Re: rappports inférieurs à 10
Salut,
Sans connaitre quoi que ce soit concernant la variable a (et, dans une moindre mesure, les autres) on ne peut pas dire grand chose : essaye avec a=150,23 ou bien -a=-0.012 voire a=-3,14159 . .
Sans connaitre quoi que ce soit concernant la variable a (et, dans une moindre mesure, les autres) on ne peut pas dire grand chose : essaye avec a=150,23 ou bien -a=-0.012 voire a=-3,14159 . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: rappports inférieurs à 10
Merci pour la réponse
a,b,c,d sont les chiffres d'un dividende et ABC les chiffres d'un diviseur
si le diviseur a trois chiffres et que les 3 premiers chiffres du dividende forment un nombre inférieur au diviseur, alors on prend les quatre chiffres du dividende. Un nombre de quatre chiffres est forcément supérieur à un nombre de trois chiffres.
Et je pense que le rapport euclidien de ce nombre de quatre chiffres par le diviseur de trois chiffres est inférieur à 10
cette question (et sa réponse) me permettrons de justifier mon algorithme de division
Cordialement
a,b,c,d sont les chiffres d'un dividende et ABC les chiffres d'un diviseur
si le diviseur a trois chiffres et que les 3 premiers chiffres du dividende forment un nombre inférieur au diviseur, alors on prend les quatre chiffres du dividende. Un nombre de quatre chiffres est forcément supérieur à un nombre de trois chiffres.
Et je pense que le rapport euclidien de ce nombre de quatre chiffres par le diviseur de trois chiffres est inférieur à 10
cette question (et sa réponse) me permettrons de justifier mon algorithme de division
Cordialement
Re: rappports inférieurs à 10
Et si les trois premiers chiffres du dividende forment un nombre plus grand que le diviseur, comment démontrer que le rapport est inférieur à 10 ?
Re: rappports inférieurs à 10
Si toutes tes variables sont des chiffres (i.e. des entiers de 0 à 9) alors

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: rappports inférieurs à 10
Car  est un chiffre donc
est un chiffre donc  .
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: rappports inférieurs à 10
Merci beaucoup, ça marche.
Peut-on généraliser ce cas (n'importe quel nombre de chiffres pour le dividende et le diviseur) ?
Peut-on généraliser ce cas (n'importe quel nombre de chiffres pour le dividende et le diviseur) ?
Re: rappports inférieurs à 10
Soit 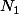 un dividende de n chiffres :
un dividende de n chiffres :

Soit un nombre constitué des n-1 premiers chiffres de
un nombre constitué des n-1 premiers chiffres de 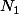

 , le diviseur, est un entier tel que
, le diviseur, est un entier tel que 
on constate que
comme
 car
car 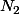 et
et  sont des entiers
sont des entiers


comme

comme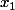 est un chiffre,
est un chiffre, 


comme
alors
donc , cqfd
, cqfd
ai-je raison ?
Soit
on constate que
comme
comme
comme
comme
alors
donc
ai-je raison ?
Re: rappports inférieurs à 10
Je me suis gouré, il faut remplacer 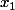 par
par 
Soit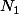 un nobre entier de n chiffres
un nobre entier de n chiffres

Soit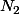 le nombre constitué des n-1 premiers chiffres de
le nombre constitué des n-1 premiers chiffres de 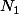

 , le diviseur, est un entier tel que
, le diviseur, est un entier tel que 
on constate que
comme
 car
car 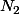 et
et  sont des entiers
sont des entiers


comme

comme est un chiffre,
est un chiffre, 


comme
alors
donc , cqfd
, cqfd
Soit
Soit
on constate que
comme
comme
comme
comme
alors
donc
Re: rappports inférieurs à 10
Si on veut diviser 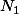 par
par 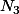 et que la différence du nombre de chiffres de
et que la différence du nombre de chiffres de 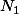 et de
et de 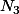 est supérieur à 1,
est supérieur à 1,
on prend le nombre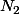 au minimum des premiers chiffres de
au minimum des premiers chiffres de 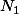 tel que
tel que  et on ne considère pas les autres chiffres de
et on ne considère pas les autres chiffres de 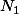 . Puis on concatène les autres chiffres de
. Puis on concatène les autres chiffres de 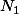 au reste et on redivise.
au reste et on redivise.
Par exemple :
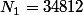 et
et 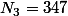 , on considère 348 et on fait la division (il y va une fois reste 1), puis on ajoute les chiffres restants, en l'occurrence les chiffre 2 et 1, au reste, ce qui donne 121 et on redivise, si ce reste est supérieur à
, on considère 348 et on fait la division (il y va une fois reste 1), puis on ajoute les chiffres restants, en l'occurrence les chiffre 2 et 1, au reste, ce qui donne 121 et on redivise, si ce reste est supérieur à 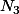 , sinon 121 est le reste
, sinon 121 est le reste
on prend le nombre
Par exemple :
Re: rappports inférieurs à 10
Excuse-moi Ben314, mais je me suis gouré dans les hypothèses :
on a le dividende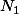
on a
on a le diviseur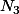

et on cherche à savoir si
quelqu'un a une idée?
on a le dividende
on a
on a le diviseur
et on cherche à savoir si
quelqu'un a une idée?
Re: rappports inférieurs à 10
Bonjour
Il faudrait un énoncé clair indiquant ce que l'on suppose et ce que l'on cherche à démontrer...
Il est évident que si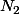 est défini comme
est défini comme  où
où  est le chiffre des unités de
est le chiffre des unités de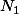 , avec un
, avec un 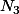 quelconque, on n'aura pas nécessairement
quelconque, on n'aura pas nécessairement 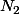 /
/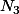 <10,
<10,
par ex :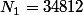 et
et 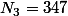
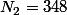 1
1

En fait, dans une division on choisit le nombre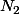 , de sorte que
, de sorte que 
avec où p est à déterminer (dans l'exemple précédent p=2)
où p est à déterminer (dans l'exemple précédent p=2)
Il faudrait un énoncé clair indiquant ce que l'on suppose et ce que l'on cherche à démontrer...
Il est évident que si
par ex :
En fait, dans une division on choisit le nombre
avec
Re: rappports inférieurs à 10
Je vais essayer de remettre tout ça en ordre :
le diviseur N3 a n chiffres.
N2, le nombre des n premiers chiffres du dividende tel que . Avons-nous
. Avons-nous 
si alors on prend
alors on prend 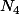 qui a n+1 chiffres. Avons-nous
qui a n+1 chiffres. Avons-nous 
le diviseur N3 a n chiffres.
N2, le nombre des n premiers chiffres du dividende tel que
si
Re: rappports inférieurs à 10
emmesse a écrit:catamat a écrit:par ex :et
1
car
ce n'est pas ça ?
Certes , ce que je voulais dire c'est que pour cet exemple; on a :
et non pas
Par contre je suis OK pour dire que le nombre de chiffres de N2 est n ou n+1, n étant le nombre de chiffres du diviseur.
On choisit l'un ou l'autre de sorte que 1<= N2/N3 <10
Re: rappports inférieurs à 10
Pour diviser  par
par  où
où  a
a  chiffres (et
chiffres (et  en a au moins
en a au moins  ), on considère le nombre
), on considère le nombre  formé des
formé des  premiers chiffres de
premiers chiffres de  puis,
puis,
- Soit et on a évidement
et on a évidement  vu que
vu que  a un chiffre de moins que
a un chiffre de moins que  .
.
- Soit et on prend un chiffre de plus dans
et on prend un chiffre de plus dans  :
:  où
où  est un chiffre et on a alors
est un chiffre et on a alors  vu que
vu que  a un chiffre de moins que
a un chiffre de moins que  ainsi que
ainsi que \!+\!c<10B) .
.
- Soit
- Soit
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
