Thermodynamique transformation isochore
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Sep 2023, 16:18
par novicemaths » 19 Sep 2023, 16:18
Bonjour
On considère une transformation isochore.
Je dois montrer que
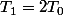
avec


avec dv =0 donc W=0
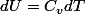
Avec

On en déduit

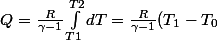)
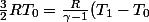)
j'ignore si je dois commencer mon calcul ainsi.
A bientôt
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Sep 2023, 19:01
par novicemaths » 19 Sep 2023, 19:01
J'ai peut-être trouvé la solution

On met d'abort sous le même dénominateur
} = \frac{RT_1}{2(\gamma-1)} - \frac{RT_0}{2(\gamma-1)})
Là, je ne suis pas du tout sûr de mon raisonnement.
}=-\frac{3RT_0}{2(\gamma-1)}- \frac{RT_0}{2(\gamma-1)})
}=\frac{3RT_0}{2(\gamma-1)}- \frac{RT_0}{2(\gamma-1)})

On retire les R.
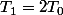
A bientôt
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Sep 2023, 20:23
par novicemaths » 19 Sep 2023, 20:23
Après réflexion, j'ai fais n'importe quoi ci-dessus.
J'ignore si c'est une erreur de l'énoncé.
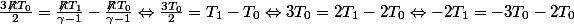
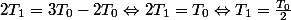
Est-ce que j'ai bien appliqué les règles de calculs ?
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 20 Sep 2023, 08:29
par Pisigma » 20 Sep 2023, 08:29
Bonjour,
je ne réponds qu'à ton développement
novicemaths a écrit: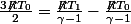
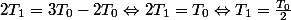
Tu devrais quand même faire gaffe quand tu réduis au même dénominateur car c'est faux!
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 20 Sep 2023, 20:55
par novicemaths » 20 Sep 2023, 20:55
Bonsoir
Je vais bien reposer l'opération depuis le début.

La partie droite

et

sont bien sous le même dénominateur.
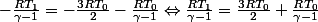
Est-ce jusque là c'est correct ?
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 20 Sep 2023, 21:12
par Pisigma » 20 Sep 2023, 21:12
novicemaths a écrit:Bonsoir
Je vais bien reposer l'opération depuis le début.
La partie droite

et

sont bien sous le même dénominateur

pas du tout!, tu ne sais pas réduire 3 fractions au même dénominateur???
c'est quand même assez élémentaire, non?
quel cursus suis-tu? tu es en quelle année?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 20 Sep 2023, 21:33
par novicemaths » 20 Sep 2023, 21:33
J'ai réussi à entrer en licence sans bac.
Là, j'espère que c'est correct.
} = \frac{3RT_0(\gamma -1)}{2(\gamma -1)} + \frac{2RT_0}{2(\gamma -1)})
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 20 Sep 2023, 21:43
par Pisigma » 20 Sep 2023, 21:43
continue un peu ton calcul
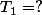
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 23 Sep 2023, 23:20
par novicemaths » 23 Sep 2023, 23:20
Bonsoir
Je bloque au niveau du calcul.
 + 2RT_0)
, je pourrai essayer de développer

Le

me pose du souci.
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 24 Sep 2023, 07:00
par Pisigma » 24 Sep 2023, 07:00
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 24 Sep 2023, 15:48
par novicemaths » 24 Sep 2023, 15:48
Bonjour
Avec

et
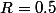
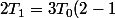 + 2 \times 0.5 T_0= 6T_0-3T_0 +1T_0 =3T_0+T_0 =4T_0)

Est-ce que c'est correct ?
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 24 Sep 2023, 16:45
par Pisigma » 24 Sep 2023, 16:45
oui
tu dois être plus sûr de toi quand tu "fais" des calculs , tu peux souvent les vérifier par toi-ême
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 25 Sep 2023, 15:23
par novicemaths » 25 Sep 2023, 15:23
Bonjour
J'ai une nouvelle question concernant la transformation isochore.
Exprimer le volume 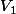 en fonction de
en fonction de 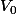 .
.J'ai essayé de voir si je pouvais répondre à question avec le graphique ci-dessous.
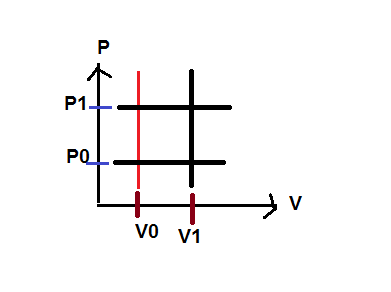
Où alors on utilise la loi de Charles.
Soit

ou

Où les gaz parfaits.
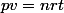
que l'on transforme en
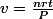
Si j'ai bien compris le volume est constant pour une transformation isochore.
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Sep 2023, 16:23
par Pisigma » 25 Sep 2023, 16:23
si tu n'as pas de cours sur les transformations thermodynamiques
tu pourrais en trouver sur la toile
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 13 Sep 2024, 22:16
par novicemaths » 13 Sep 2024, 22:16
Bonsoir
La loi de Charles peut s'écrire sous la forme.

L'expression de

en fonction de
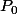
est:

Est-ce que c'est correcte ?
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
et
sont bien sous le même dénominateur

