Bonjour,
Je suis en premières spé maths et je bloque sur un exercice sur les dérivations/suites.
Voici le sujet :
On considère une boîte de conserve de forme cylindrique. Un volume V étant donné, on souhaite minimiser la quantité de métal utilisé pour fabriquer cette boîte.
On note r : le rayon de la base et h : la hauteur.
1. Démontrer que la surface de métal utilise est donnée par S(r) = 2πr^2 +2V/r (fait)
2. Donner l’ensemble de définition de S et étudier les variations de S sur ce domaine. (fait)
3. En déduire les dimensions de la boite répondant au problème posé.
Je bloque sur la question 3.
Merci d'avance pour votre aide !
DM Maths 1ere - Dérivation/suites
6 messages
- Page 1 sur 1
DM Maths 1ere - Dérivation/suites
Modifié en dernier par arnoox le 29 Déc 2020, 17:18, modifié 1 fois.
Re: DM Maths 1ere - Dérivation/suites
bonjour,
question 2: quelle est la ou les valeur(s) de r qui sont interdites ?
Ensuite, il s'agit de calculer la dérivée de S par rapport à la variable r.
question 2: quelle est la ou les valeur(s) de r qui sont interdites ?
Ensuite, il s'agit de calculer la dérivée de S par rapport à la variable r.
Re: DM Maths 1ere - Dérivation/suites
Bonjour à vous,
En fait, ce que je n'ai pas compris, c'est qu'il n'y a pas de valeur. C'est a dire qu'il y a seulement des lettres et pas de nombre et c'est ça que je ne comprend pas.
Mais je vous remercie pour votre aide
En fait, ce que je n'ai pas compris, c'est qu'il n'y a pas de valeur. C'est a dire qu'il y a seulement des lettres et pas de nombre et c'est ça que je ne comprend pas.
Mais je vous remercie pour votre aide
Re: DM Maths 1ere - Dérivation/suites
En quoi "des letters" posent-elles un problème ? Les lettres représentent des valeurs, le seul truc c'est qu'on ne les connaît pas a priori, ce sont des "indéterminées".
Ce que vous allez trouver sera donc une condition pour que ce soit toujours vrai : pour tout volume V, vous allez obtenir la quantité minimale de métal. Si plus tard on vous dit que V=1 centimètre cube, vous direz "la quantité de métal est...".
Comme dans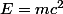 d'Einstein : pas de valeur (sauf c en fait) que des lettres. Mais si on me donne m, alors je sais calculer E et si on me donne E, je sais calculer m.
d'Einstein : pas de valeur (sauf c en fait) que des lettres. Mais si on me donne m, alors je sais calculer E et si on me donne E, je sais calculer m.
Dons votre problème : vous avez fait la question n°2. Qu'avez-vous trouvé ?
Ce que vous allez trouver sera donc une condition pour que ce soit toujours vrai : pour tout volume V, vous allez obtenir la quantité minimale de métal. Si plus tard on vous dit que V=1 centimètre cube, vous direz "la quantité de métal est...".
Comme dans
Dons votre problème : vous avez fait la question n°2. Qu'avez-vous trouvé ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM Maths 1ere - Dérivation/suites
arnoox a écrit:2. Donner l’ensemble de définition de S et étudier les variations de S sur ce domaine. (fait)
S est définie pour
la dérivée de la dérivée (on dit "la dérivée seconde")
On note que S'' est (strictement) positive.
Annuler la dérivée. Quelle relation obtient on entre r et V ?
Calculer h en fonction de r au point où la dérivée S' s'annule. Il s'agit d'un minimum pour S.
Re: DM Maths 1ere - Dérivation/suites
S est minimale pour les valeurs de x telles que S'(x)=0. Résolvons cette dernière équation.
=0 \leftrightarrow 2\pi r^3=V=\pi r^2 h)
Soit
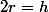
Soit D le diamètre du fond de la boite.
S est minimale pour h=2r=D.
L'aire de la surface est minimale ssi la hauteur est égale au diamètre du fond de la boite.
Soit
Soit D le diamètre du fond de la boite.
S est minimale pour h=2r=D.
L'aire de la surface est minimale ssi la hauteur est égale au diamètre du fond de la boite.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
