Forme explicite d'une suite

[pierrelouisbourgeois]

Bonsoir,

Je ne parviens pas à donner la formule explicite de Un+1 = Un - n

Est-ce que vous pourriez-m'aider ? Merci

[pascal16]

U1=U0-0
U2= U1-1= Uo-(0+1)
U3=U2-2=Uo-(0+1+2)

toujours pas ?

[pierrelouisbourgeois]

Non désolé..

[pierrelouisbourgeois]

D'ailleurs est-ce que c'est une suite arithmétique ?

[lyceen95]

D'après toi ?
Quelle est la définition d'une suite arithmétique ? Cette suite respecte-t-elle cette définition ?

Mais ce serait bien que tu reopies l'énoncé complet de l'exercice, parce que la suite dont tu parles, elle n'est que partiellement définie.
Tu as du mal à étudier une suite, et en fait tu es en train d'étudier une famille de suites. Gros challenge !

[pierrelouisbourgeois]

Alors je dois étudier le sens de variation ; d'ailleurs U0 = 2

[pierrelouisbourgeois]

Si c'est une suite arithmétique elle a la forme : Un+1 = Un + r ; Or ici je ne sais pas si r correspond à une constante ou si on peut dire que r = -n mais j'en doute...

[pascal16]

il faut voir plus loin

U3=U2-2=Uo-(0+1+2)
Un= Uo-(0+1+2+3+4...+n)

(0+1+2+3+4...+n) sont les termes d'uns suite arithmétique, on sait exprimer cette somme
Un elle-même n'est pas arithmétique (la différence entre deux termes consécutifs varie)

[pierrelouisbourgeois]

Un = U0 - (n(n+1))/2 ?

[pierrelouisbourgeois]

Pardon c'est plutôt Un = Uo - (n^2-n)/2

[lyceen95]

Définition d'une suite arithmétique, prise sur Wikipedia :
En mathématiques, une suite arithmétique est une suite (le plus souvent une suite numérique) dans laquelle chaque terme permet de déduire le suivant en lui ajoutant une constante appelée raison.

C'est une phrase en français, c'est pas un truc du genre Un+1=Un+r.
Un+1 =Un+r, tout seul comme ça, ça ne veut rien dire.
Pour que ce truc ait un sens, il faut ajouter des symboles ou 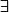aux bons endroits.

Et dans cette définition, il y a le mot 'Constante'.

[Noemi]

Bonsoir pierrelouisbourgeois,

Un = Uo -(0 + 1 + 2 + 3 + .... + (n-1))
Donc
Un = Uo - n(n-1)/2 est bien le résultat

[pascal16]

dsl pour l'erreur d'indice