Caractériser un ensemble à l'aide d'une valeur absolue
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 30 Oct 2019, 13:11
par LB2 » 30 Oct 2019, 13:11
Bonjour Emma,
|a-b| représente la distance entre les réels a et b sur la droite réelle.
L'ensemble des x vérifiant l'inéquation |x-1| <= 2, par exemple, est l'ensemble des réels à distance <= 2 du point 1.
Donc le segment [-1,3]
Noter que comme la valeur absolue est une fonction paire, l'inéquation |1-x| <= 2 donnerait le même ensemble de solutions.
Lorsque l'inéquation est dans l'autre sens, par exemple |x-2| >= 5, on trouve comme solutions l'union de deux intervalles de R : ]-infini, -3] union [7, + infini[
Fais a chaque fois une représentation graphique de la droite réelle pour t'aider à visualiser l'ensemble des solutions de chaque inéquation.
Dernière astuce : |x| = |x-0|
Bon travail!

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 30 Oct 2019, 15:41
par capitaine nuggets » 30 Oct 2019, 15:41
Salut !
Pour ton premier exercice, de façon générale, quels que soient les nombres

et

, on a toujours les propriétés suivantes :
1)
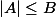
équivaut à
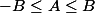
;
2)
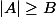
équivaut à
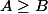
ou
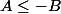
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
 )
)